投稿者: みかん先生

息子が九州に帰ってから５日たちました。すっかりむこうの生活にも慣れたかなぁ～なんて思っていたら、本日泣きながら息子から電話ありました。そのワンシーンです。

“離れた息子の近況。” の続きを読む

はじめまして。

指導の対象を「算数数学が苦手な子」に限定しているみかん先生と申します。

現在、東京２３区を中心に活動させて頂いております。このページではみかん先生の概要を説明したいと思います。

“算数数学が苦手なお子さんをお持ちの親御さんへ” の続きを読む

指数関数のグラフを学習した後は、累乗根の大小の学習です。
累乗根どうしにも大小がある！ということを意外と忘れがちです。
板書はこれまでの大小の話から入り、
その値の大きさをイラスト調で示しています。
もちろん、大小の根拠となるグラフも吹き出しでしめしています。

僕はこれまでみてきた「算数・数学のセンスが抜群の子」に1つ共通していることがあります。それは彼らが目の前の問題を圧倒的なスピードで解くのではないということ。

“優れた数のセンスをもつ子は、何がちがうのだろう？” の続きを読む

子どもたちから尊敬されたい、と思ったことがありません。
尊敬はされなくていいんです。尊敬されることを考え始めたら、むしろ授業は上手くいかない気がします。
子どもたちの良き理解者であり、彼ら彼女らの成長を心から願う１人でありたい。
僕が願うのはそれだけです。
「みかん先生って、普通だよ。
　違うところはよく話を聞いてくれるぐらいかな。
　僕が勉強できるようになったのは、僕の力なんだ。
　先生のおかげじゃないよ。これは僕の力なんだ。」
もしこんな会話が生まれることが、僕の目指すべきゴールだと思います。
そこに＜みかん先生の力＞とかいらないのです。
ただし、こんな会話が繰り広げていられたら？
「みかん先生の授業って分かりやすい。
　先生がいてくれたから私は数学ができるようになった！」
会話は嬉しいのですが、こんな僕には修行が必要です。
僕が誉められちゃいけない。本人が誉められている間は「みかん先生」は未熟です。

僕の授業はできる限り覚えることを少なくしています。結果的に応用も利くためそうさせています。具体的にどういったものか簡単に説明します。
■具体例
ここに計算方法１つ、公式４つがあります。
【一般的な数学で覚えること】

多項式の計算
(ｘ+a)(ｙ+b)＝ｘy+bｘ+aｙ+ab

乗法公式
・(ｘ+a)(ｘ+b)＝ｘ²+(a+b)ｘ+ab
・(ｘ+a)²＝ｘ²+2aｘ+a²
・(ｘ-a)²＝ｘ²-2aｘ+a²
・(ｘ+a)(ｘ-a)＝ｘ²-a²

この公式は中学3年生で学校でも塾でも暗記させます。
これが苦手な子を専門指導する僕の授業だとこうなります。
【みかん先生の数学で覚えること】

・(ｘ+a)(ｙ+b)の展開イメージする。
・２つのカッコに同じ項があれば特別になる。

覚えることを２つまで減らしています。
数学が苦手な子は、多くの公式や解法を覚えると解き方の混乱が起こります。このように覚えることを少なくすることで、記憶の負担を減らしています。

苦手な子へのイメージを使った学びについて簡単に説明します。
その前に、まずはよくある学習形式を説明した後に、僕が行う図で教える方法(図式)を説明します。
■1-1.よくある学習形式【式を見せる】
まず、子ども(学習者)に問題を見せます。
そして子どもなりに仮説を立てるはずです。

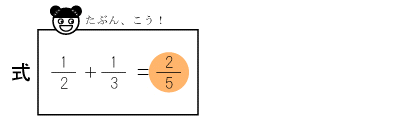
そしてこのあとで計算手続きを教えます。

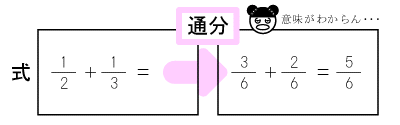
しかしこれでは子どもは納得できません。
なぜなら、明らかな自分なりの仮説があったからです。
そこでみかん先生の教え方をご紹介します。

---

■2-1.図式のアプローチ【図から出発】
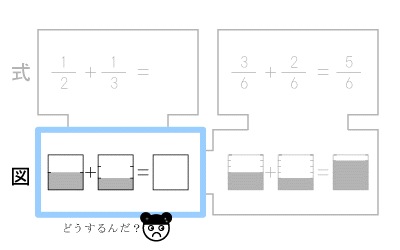
図式では、はじめに図(イメージ)を与えます。
イメージ確認が、何よりも大切だと考えているからです。
そして次に
「この図を分数の式で表現してみよう。」
と子どもに出題します。
イメージから数が、算数数学の第一歩です。
■2-2.図式のアプローチ【図から式へ】

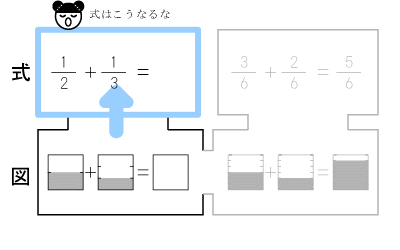
そして子どもが図(イメージ)を分数で表現します。
ここで初めて未知の分数のたし算を、
目で確かめます。
もちろん、
「５分の２になるんじゃないか？」
という予測もありです。
子ども達の自由な発想を、
ここで押さえつけるようなことはしません。
■2-3.図式のアプローチ【式から図へ】
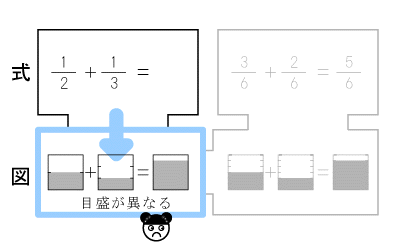
そしてこの式の答を探るために、
ここで、もう一度、図にもどってみるように促します。
なぜならたし算の本質的な意味を、
この図で確認できるからです。
「２つをたしたら、結構、いっぱいになる！」
これに気づけば、
「５分の２という答は違うなぁ･･･」
と検討がつきます。
そしてなぜ、答が分からないのか？
本質的な課題に直面します。
「２つの目盛が違うから、
　どのくらいになるのか分からないのか」
と小さな発見をします。
大人からみれば当たり前のこと。
しかしこの気づきこそが、分数の要なのです。
■2-4.図式のアプローチ【本質理解を得る】
目盛が違うから分からない･･･
ここまでくれば、
「目盛がそろえればい い」
という発想が出てくるのは時間の問題です。
まずは、自分で図に目盛をふる。
そして本当にその目盛であっているのか、
何度も自分で確認します。
このようなたった数秒の確認行為が
「本質理解」を手に入れるのです。
■2-5.図式のアプローチ【方法を知らずに導く】
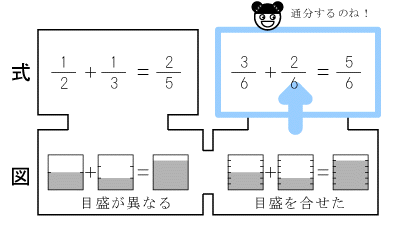
目盛が合ったところで、
今度は図を式で表現します。
ここで現れる式は、通分された式です。
答も図を使って、方法を知らぬままにできました。
この
「方法を知らずにできた」
という経験が大切です。
その経験の後、初めて「通分」の話が生きてきます。
(通分のアプローチは省略します)
■2-6.僕のアプローチ【算数力の理想】
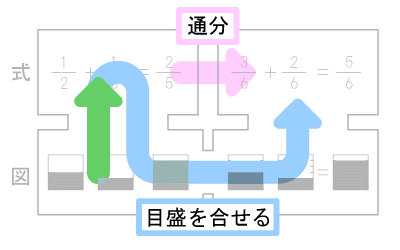
“通分”とは「方法」
“目盛を合せる”とは「理解」
これらが２つあって始めて算数力は身につきます。
そしてお気づきの方もいるかもしれません。これまでのアプローチは、「概念」「理解」「方法」すべてを踏まえています。こういったことが「算数力の理想」になるのです。

このアプローチは概念→理解→方法という流れをしっかり組んでいるのです。
だから子どもも無理なく方法を吸収できます。
けっして方法の一方通行ではない。
概念から、理解。そして方法へと進む。
図で考えるとは、傍からみれば無駄な寄り道のような気がします。
しかし理想的な算数(数学)の歩み方なのです。
■3.図式の由来【※補足】
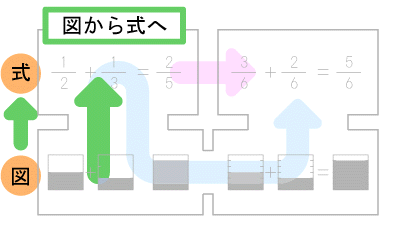
私が唱えている「図式」とは、このアプローチの重要な箇所、図から式にすすむ過程、を表しています。
概念の確認は、子どもに教える上でもっとも重要なことです。
それを肝に銘じるために、図式、と呼んでいます。

８月に産まれる娘のために名前を考え中ですが、わが家は名づけが拘りなく単純です。わが子の名前だから親の願いを！というわけではないちょっと今や変わった名づけ方。

“親の願い込めるべき？シンプルな僕の名づけ。” の続きを読む

世の中にはどうも理解できないことがあります。
「ご家庭のシンクの上戸棚に、何が入っているか？」
ふつうはキッチン関係の食料保存品とか、キッチン器具などが入るものですが、わが家では少し違う。 “シンクの上の戸棚に何が？価値観が生んだ収納。” の続きを読む

子どもにお菓子を１つあげて、それで済むはずはないのですが。泣きじゃくった息子を見て、気づかされたことがありました。そんなツラツラ文章です。

“一粒のお菓子。日曜日、親子の合戦。” の続きを読む