このページでは、小学3年生の各単元におけるみかん先生の教え方（サポートの仕方）をQ&A形式で紹介してます。
◯目次
- かけ算のきまり
- 時こくと時間の もとめ方
- わり算
- たし算とひき算の筆算
- 長いものの長さのはかり方と表し方
- 暗算
- あまりのあるわり算
- 大きい数のしくみ
- かけ算の筆算(1)
- 大きい数のわり算， 分数とわり算
- 円と球
- 小数
- 重さのたんいと はかり方
- 分数
- □を使った式
- かけ算の筆算(2)
- 三角形と角
- ぼうグラフと表
※タイトル・指導時間数・ページ・学習指導要領の指導項目については、東京書籍の「年間指導計画 略案（3年）」を参照してます。
1.かけ算のきまり
「九九を見なおそう」
想定される学校の授業時数：約9時間
【学習する知識】なし
Q.九九を２つにわけて計算する理屈がわかりません！
しきりを作って考えます
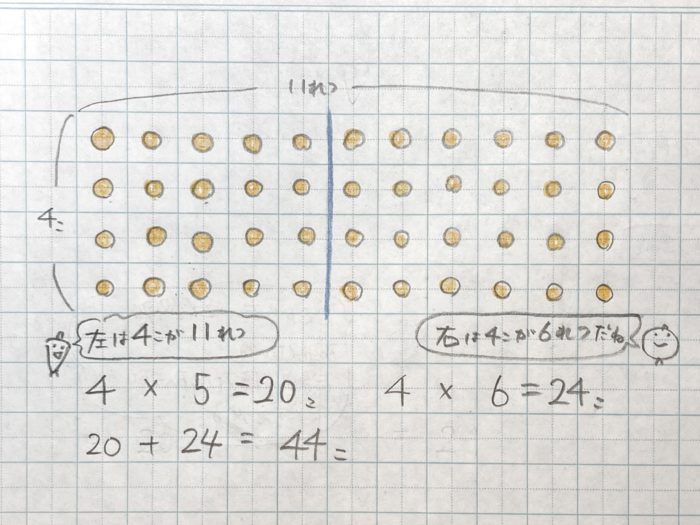
並んでいる数が9こまでなら、九九を使って解けます。このような10以上のもの並びは、「しきり」を入れて10より少ない並びに変えることで求められます。
Q.「０×３」や「５×０」などの０のかけ算が分からない。
かけ算のイメージに戻ります
九九を学んだ後、かけ算の概念が曖昧になります。もう一度、かけ算はどこの数をもとめるものなのか？図をもとにして振り返ります。２×３の答６は全体の量を表します。０×３の答も同じです。まんじゅうが１皿に０こある。これを３皿用意したときの全体の量を図をみて考えます。
2.時こくと時間の もとめ方
「時こくと時間のもとめ方を考えよう」
想定される学校の授業時数：約4時間
【学習する知識】秒
Q.時刻は分かるが、時間がピンときてません。
時間の存在を色で表します
時刻は見える文字盤の数字を読めばいいだけですが、時間にはそれがありません。時間は、時刻と時刻の間にある目盛りの個数です。
その目盛りの個数で「時間が長い・短い」と言います。まだ時間の概念が弱いときは、文字を色でぬって時間の存在を明らかにします。
時計の長針だけを表示した「時間をもとめる」プリントです。スモールステップで練習できますよ。
時間を求める補助プリント
Q.3時20分の10分前というと「3時30分」と後の時刻になってしまいます
「時間の前後」は「私たちの前後」と反対になることを説明します
このつまずきが起こる理由は、時計の針を自分自身に投影しているからです。「10分前」というのは、針が向かっている前ですから20分より10分先の3時30分となります。これはよくある間違いです。
この躓きについては「時刻の前後が分からない子どものいい分」で詳しく紹介しています。
Q.午後2時10分の30分前などの「12」をまたぐ時間がわかりません
時間の筆算をつかいます
長針と短針が文字盤の12をまたぐと、分を表す長針・時間を表す短針どちらにも繰り上り（繰り下がり）がおこります。それが一部のお子さんにとって、ややこしいです。このような場合、時間の筆算をつかう方法を練習します。
Q.80秒が何分何秒か分かりません
80秒から60秒を作ります
時間の概念が弱い子は、時間のくり上がりの認識もあいまいです。
- 60秒は1分に変わることを理解します。
- 80秒は60秒より大きい数です。80秒の中に60秒が隠れています。80秒を60秒と20秒に変えます。
- 60秒を1分に変えて、1分20秒です。
これは２桁のわり算を習っていない状態での求め方です。4年生になるとわり算を使って求められます。
3.わり算
「同じ数ずつ分けるときの計算を考えよう」
想定される学校の授業時数：約9時間
【学習する知識】÷,わり算,わる数,わられる数
Q.わり算の考え方がわかってないようです
わられる数→わる数の順をイメージで示します
わり算は、どのような数を求めたいときに使われるものなのか。これをたし算やひきざん、そしてかけ算を含めてイメージで違いを学びます。それでも難しい子の場合、イメージの凡例を用意して丁寧に判別できるように練習します。
Q.“何人にわけることができますか？”の問題がわり算だとわかりません
「何人ずつ」に注意して、わり算の違いを見比べます
わり算をつかう状況は２つあります。このわり算は包含除というものです。「〜ずつ分ける」という点に注意します。それぞれの状況をイメージで示して考えます。これらは「ドキドキわり算」と名前をつけて取り組んでます。
Q.わり算で答が思い浮かびません
はじめは九九表をみます
わり算の答を探すとき、九九を用います。このとき頭の中で唱えても、わられる数を通り過ぎてしまうこともあります。ような失敗経験を元に修正して行きますが、音から数をうまく想起できない子もいます。
その時は九九表をみて取り組みます。
4.たし算とひき算の筆算
「大きい数の筆算を考えよう」
想定される学校の授業時数：約8時間
【学習する知識】なし
Q.205+398などの繰り上りの計算ができません
繰上げの動作を分けて、ていねいに練習します
「３けたのたし算の手順」は「２けたのたし算の手順」より手数が多くなります。１、2年生でたし算の繰り上がりで躓いたお子さんは、３けたのたし算でも躓きがちです。このような場合、繰り上げの動作をまずゆっくり１つ１つ行います。
例：３けたのたし算の繰り上がり
１）１の位のたし算「５＋８」で13です。繰り上がりの10は小さく「１」と書きます。ここでひと呼吸です。
２）ゆっくりと十の位のたし算「０＋９」の答で９。それに１をたして１０です。確かめて書き込みます。
この動作を練習します。慣れればスムーズにできるようになります。
5.長いものの長さのはかり方と表し方
「長い長さをはかって表そう」
想定される学校の授業時数：約7時間
【学習する知識】きょり,みちのり,km
Q.きょりと道のりの違いがわかりません
言葉とイメージを合わせて教えます
お子さんにとって２つとも聞き慣れない言葉なので、なかなかイメージしづらいです。道のりは「道」という言葉があるので分かりやすいです。きょりは「真っ直ぐ進んだながさ」というイメージで捉えていきます。
Q.１kmの長さが感覚的にわからない
地図（グーグルマップ）をつかって調べます
cmやmといった単位はその場で示すことが可能です。しかし「1km」は、その場で見せることはできません。このような場合、１kmがどこまでか学校や駅といった身近な場所までの距離をグーグルマップ等で調べます。
6.暗算
「数をよく見て暗算で計算しよう」
想定される学校の授業時数：約3時間
【学習する知識】なし
Q.暗算の数を分けるができません
無理にやらせません
数の分解が苦手な子にとって、この暗算は計算嫌いを引き起こしますので、あまりやらせません。これまで通りの筆算を奨励します。どうしてもという場合、無理のない範囲でやってみます。
7.あまりのあるわり算
「わり算を考えよう」
想定される学校の授業時数：約7時間
【学習する知識】あまり,わりきれない,わりきれる
Q.60÷3などの式の計算で一の位の0を抜いてしまう。
一の位も必ずわる、と促します
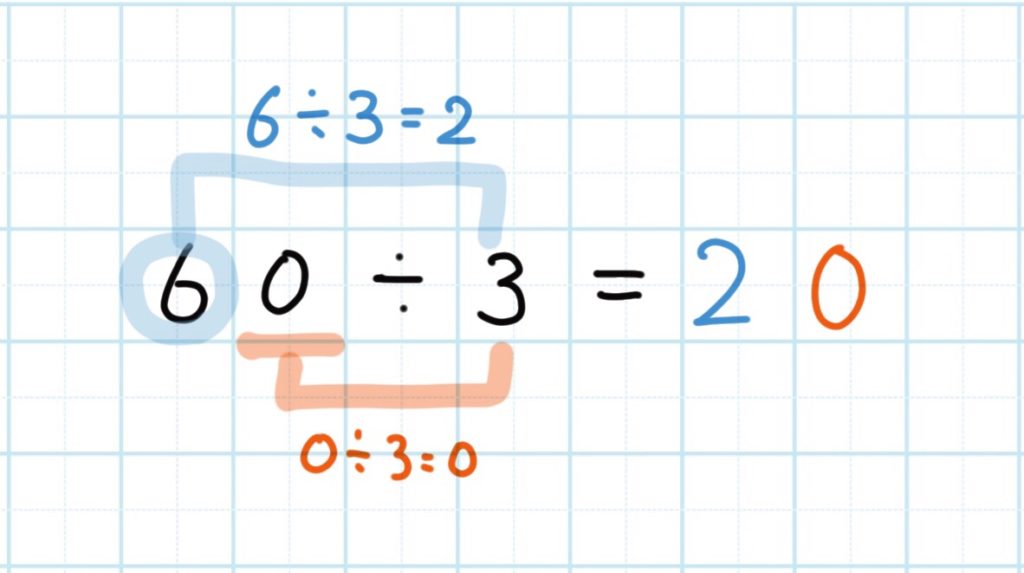
「わり算のゴールは一の位をわるところまで※1」と前提を確認します。一の位は０だから0÷3＝0。だから一の位は0がたつと分かると思います。
Q.あまりを求めるわり算のひき算でミスをする
わられる数の下にひき算の筆算を書きます
このわり算の段階では「わり算の筆算」を習っていません。ですから、余りを求めることが難しい子もいます。そこで以下のような方法で余りを求めます。
１）わる数７の九九を言い、わられる数の45より小さい答を探す。7×6＝42なので、6を＝横に書き、42をわられる数の下に書きます
2）ここで「45ー42」をひき算の筆算をつかって余りを求めます。６の横に「あまり３」と書きます。
このやり方は、わり算の筆算の予習にもなります。あまりで躓いていない子も使っていいです。
8.大きい数のしくみ
「10000 より大きい数を調べよう」
想定される学校の授業時数：約10時間
【学習する知識】十万,百万,千万,一億,数直線,等号,不等号
Q.11890059といった大きな数を読み上げることができない。
４桁おきに区切ってよみます
万進法の数の読み上げは、多くの子どもが混乱します。数の見え方を工夫します。
１）数をマスに合わせて書きます
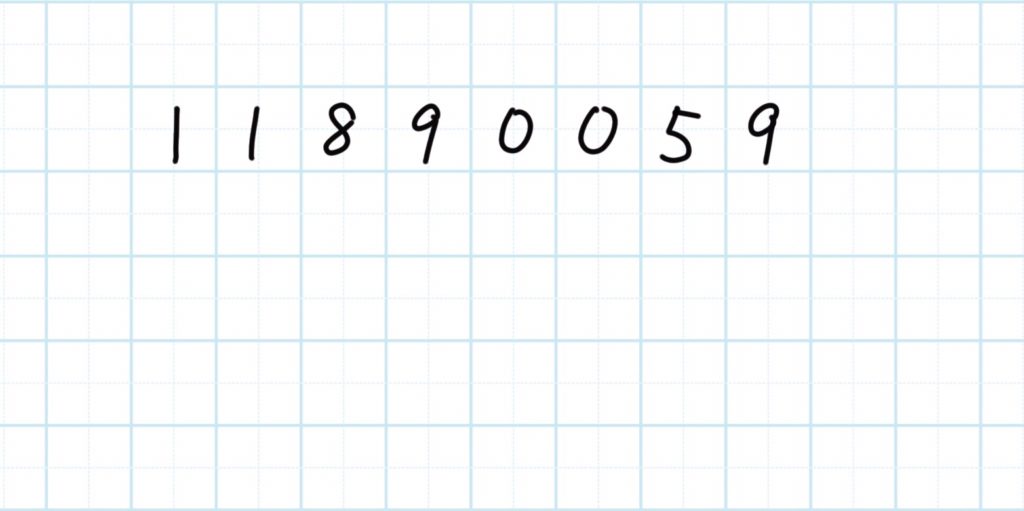
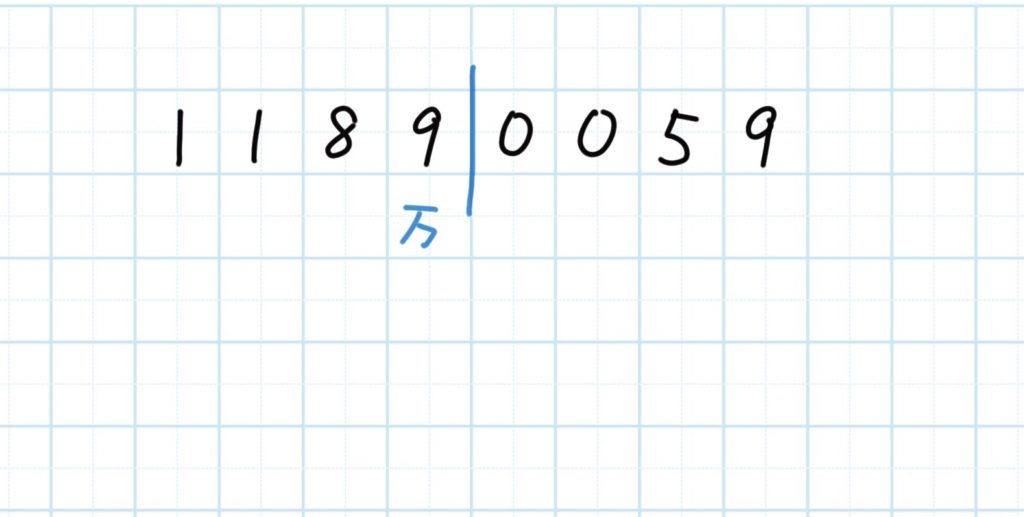
２）右から４ー５桁の間に仕切りをいれて、しきり左下に「万」と書く。
３）４桁ずつ読みその音を漢数字で書きます。
ゆったりとスペースをとって取り組むことが大切です。
Q.「二百十二万三千六百五」といった「万」を含んだ漢数字から、数に変えることができない。
万を色で分けます
漢数字を数表記に変えるにあたって整理が必要です。以下のようにします。
１）「万」に色をぬります。そして「万」より左側の数に同じアンダーラインをひきます。万の右側も別の色で線をひきます。
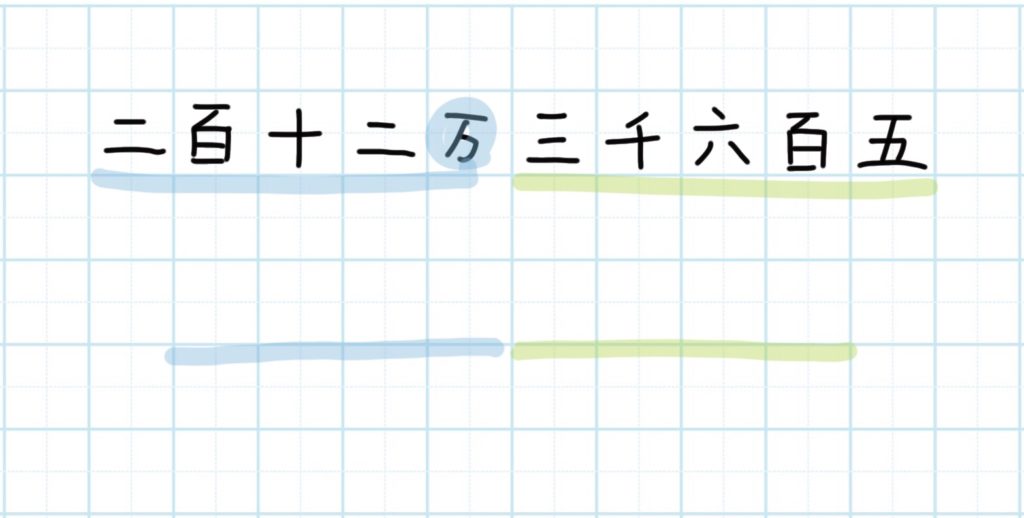
２）色別に読み上げて、数を書きます。
漢数字の通りになっているか、数字を読み上げてチェックして終わりです。
9.かけ算の筆算(1)
「大きい数のかけ算のしかたを考えよう」
想定される学校の授業時数：約11時間
【学習する知識】なし
Q.筆算の手順を間違えます
運動・視覚フォローをします
–筆算手順の間違いはよくあります。「運動フォロー」と「視覚フォロー」の両面から援助します。
運動フォロー
- お子さんの横で一緒に解く
- 手を添えて一緒に解く
- 大きい紙で解く
- 特別なレイアウトの計算用紙で解く
視覚フォロー
- 手順を番号で示す
- 手順を→で示す
- 青色鉛筆(消せるもの)に変える
Q.倍の問題で線分図が書けません
原因はさまざまです。お子さんの状況に応じてサポートを変えます
線分図が書けない理由は様々です。今回は「線分図の意味が分からない」時の説明です。
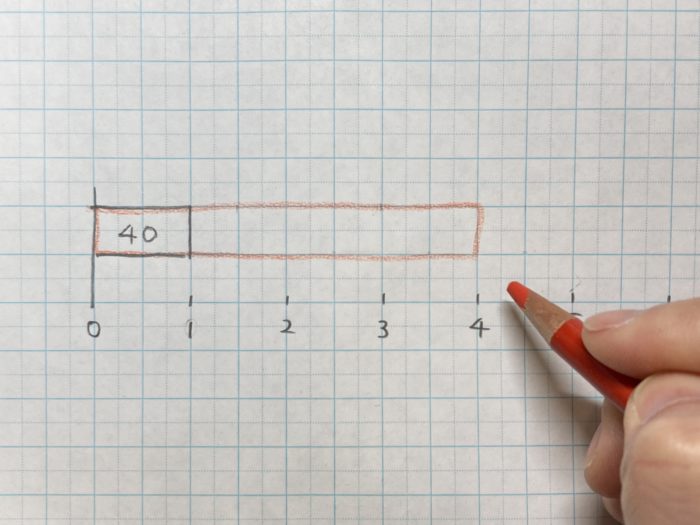
線分図の教え方
１）40の大きさを四角で表します。その4倍の大きさを赤色の鉛筆で表します。
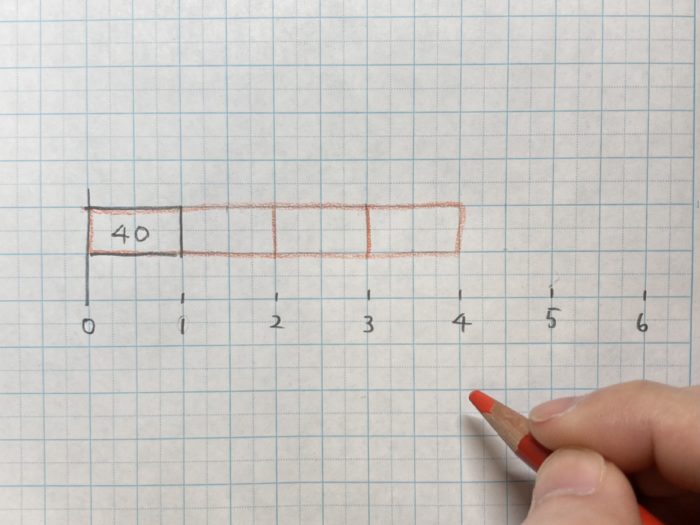
２）4倍の長さの長方形に、同じ間隔で仕切りを入れます。
３）四角の中に40を書き込みます。40が4つ分と分かります。
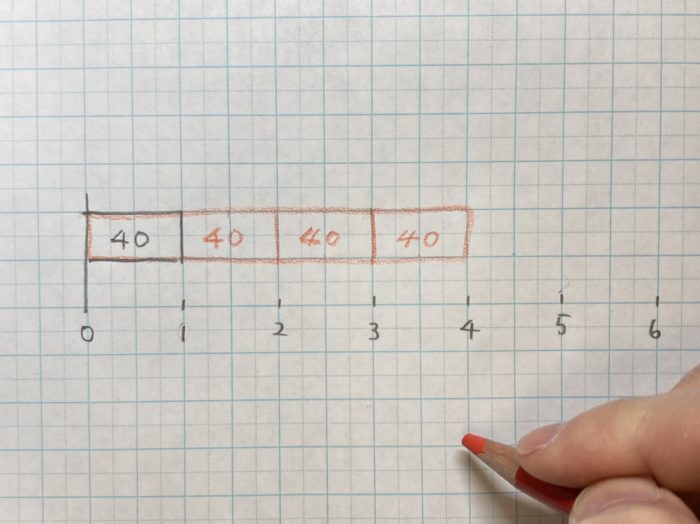
４）40が4つ分にあたる長方形の数は40×4で分かります。
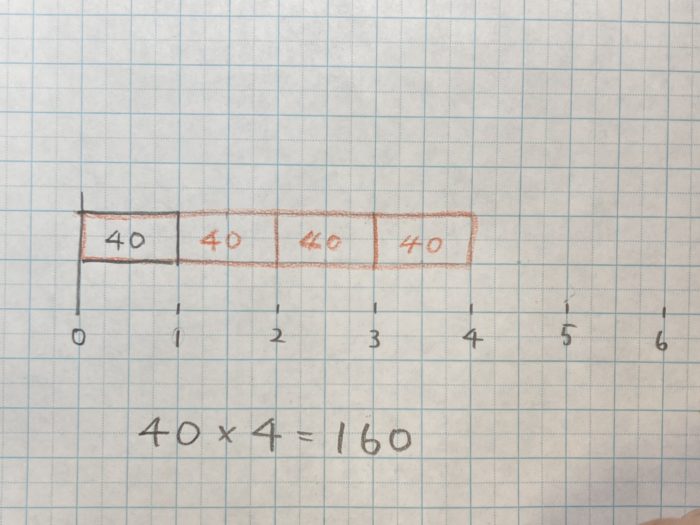
このほかにも「言語から量関係が想起できない場合」「線分図を書くスペースがない」など考えられます。状況に応じて対応します。
文章の「△は◯の３倍」の部分を３つの側面（運動・視覚・聴覚）で示して感覚で理解できるように促します。
10.大きい数のわり算， 分数とわり算
「わり算や分数を考えよう」
想定される学校の授業時数：約4時間
【学習する知識】等分する
Q.60÷3が6÷3で求められるのか分かりません
わり算のイメージから考えます
まず６まいを３人で分けるところから考えます。答えは1人２まいです。その後に10まいの束を６束を３人で分けるところを考えます。1人２束ずつになります。それぞれのわり算を式で表して、答えが同じになることを確認します。
Q.80cmの１／４の長さが分かりません
イメージは80cm÷４と同じであること確認します
まず80cm÷4人を図を使って考えます。答えは1人20cmです。
次に80cmのテープを１/４した図をかきます。１/４にあたる長さを考えると、図は同じなので20cm。80の１/４と80÷4は同じことと分かります。
11.円と球
「まるい形を調べよう」
想定される学校の授業時数：約8時間
【学習する知識】円,中心,半径,直径,球
Q.半径と直径がごっちゃになります
長さの違いを色で示します
半径は直径の半分にあたることは言葉からも類推できますが、大袈裟に色で分けて印象づけを行います。
Q.コンパスがうまく扱えません
鉛筆なし練習をします
コンパスがうまく扱えない原因の１つは、書こうとする意識がじゃまをして回転動作がうまくいかないところです。コンパスの鉛筆を外した状態で、回転させる練習をします。その後に鉛筆をつけてかきます。
補助付きのコンパスを購入してもいいです。
12.小数
「数の表し方やしくみを調べよう」
想定される学校の授業時数：約12時間
【学習する知識】0.1L,小数,小数点,整数
Q.小数0.1が1より小さいことが分かりません
0.1の大きさをイメージでつかむ
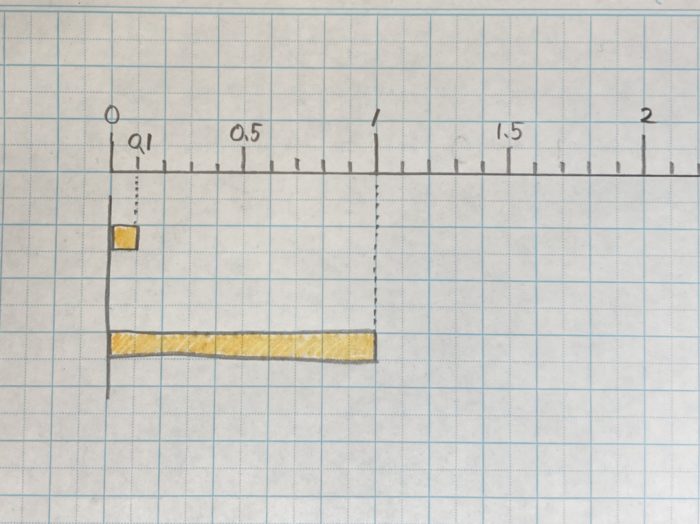
数の量のイメージが弱い子に起こる躓きです。カード等で1と0.1の大きさの違いを手にとって実感してもらいます。その上で0.2、0.5という大きさへ展開し、それでも1よりは小さいことを実感してもらいます。
Q.数直線で小数の位置がわかりません
整数に「.0」を加えて、小数かえて考えます
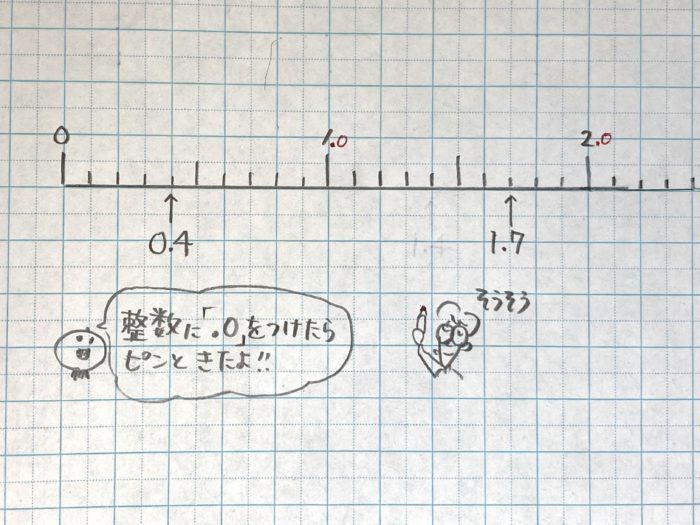
小数も整数と同じ十進法です。それがわかるように、整数をあえて小数に変えるとその仕組みが見えてきます。
Q.「1−0.6＝0.5」となってしまいます
１と0.6の数の大きさをイメージで整理します
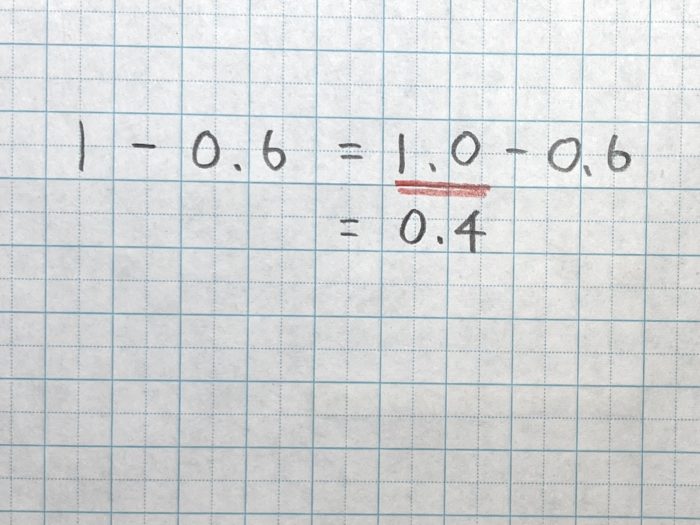
整数の１を「1.0」に変えて小数にします。桁の数を合わせると、ひき算がスムーズにできます。
13.重さのたんいと はかり方
「重さをはかって表そう」
想定される学校の授業時数：約9時間
【学習する知識】グラム,g,キログラム,kg,トン,t
Q.重さが全体的にピンときてません
はかりで重さを調べてみます
重さは長さやかさと異なり目に見えません。そこではかりを使って、いろんな重さを調べます。重さ予測などは、重さの概念「量の保存」を身につける上で効果的です。
Q.はかりの目盛りがよめません
目盛りを色分けします
目盛りの大きさがわかりにくいので、つかみにくいことが多いです。100gごとに表示されているはかりであれば、10gの目盛りを赤色で補助します。
14.分数
「分数を使った大きさの表し方を調べよう」
想定される学校の授業時数：約10時間
【学習する知識】分数,分母,分子,小数第一位,1/10の位
Q.2/3といった量がわかりません
量のイメージをかく練習をします
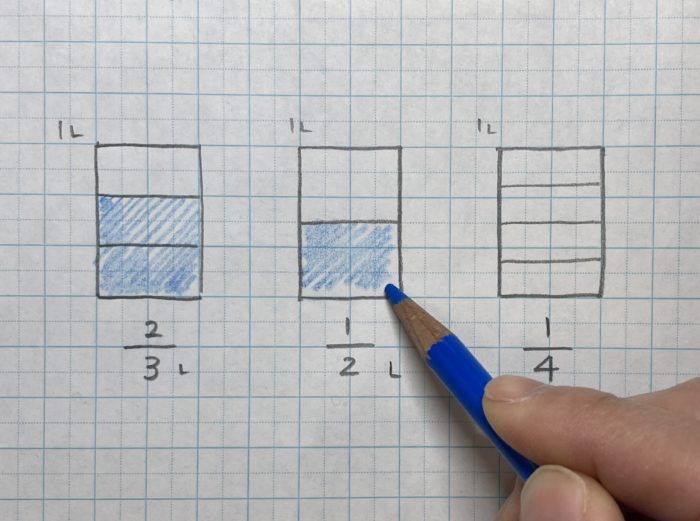
「割合分数（３年上）」と捉え方が異なるので混乱する子もいます。ここで改めて「量としての分数」をイメージで捉えます。分数のたし算・ひき算の理解にもつながるのでとても大切です。
Q.小数と分数の関係がつかめません
0.1と1/10から広げます
小数と分数はどちらも「はんぱな量」を表します。しかし２つが全く別ものと誤解しているお子さんもいます。ふたつの量をイメージでつかみつつ、同じ量を表していることを実感できるように促します。
15.□を使った式
「□を使って場面を式に表そう」
想定される学校の授業時数：約4時間
【学習する知識】なし
Q.□を使った式が立てられません
図を使って立式の練習をします
たし算・ひき算を用いる図において、□の位置は３パターンあります。たし算・ひき算の捉え方で式を３つ作れるように練習をします。
かけ算の場合も同様です。図をつかって□の位置を明らかにして、かけ算の式を作ります。
16.かけ算の筆算(2)
「かけ算の筆算を考えよう」
想定される学校の授業時数：約10時間
【学習する知識】なし
Q.２桁になると筆算の手順が分からなくなります
手順を色指示でサポートします
ワーキングメモリーが弱いお子さんは、この筆算の手順で躓くことが多いです。
まずは失敗が起こらないように、手順を色指示でサポートして練習します。慣れてきたらサポートなしで練習します。
Q.真ん中に０がある計算（604×32など）を間違えます
「0×は0」を復習して、ゆっくり計算をします
０×（×0）は、たし算の処理とごっちゃになってしまう子もいます。０の段は答が全て０になる事を思い出して、掛け算の練習をします。
Q.倍の問題で「かけ算」なのか「わり算」なのか分かりません
文章から図で関係をつかみ、かけ算の式を考えます
文章中の「□は◯の３倍」といった部分がどのようなイメージになるのか線分図等で考えます。
その後、数を当てはめて、かけ算の関係式をつくります。
その流れに一貫することで、間違えなく取り組めます。
17.三角形と角
「三角形を調べよう」
想定される学校の授業時数：約8時間／
【学習する知識】二等辺三角形,正三角形,角
Q.角の大きい・小さいが分からない
口を大きく開けているのは？でとらえます。
角の概念はなかなか難しいです。角というのは「ひらき具合」です。そこで角の外側を擬人化して「口を大きく開けている」という部分に注目して角の存在を認識するようにします。慣れてきたら、辺の長さを変えて角の大きさを考えます。
18.ぼうグラフと表
「わかりやすく整理して表そう」
想定される学校の授業時数：約10時間
【学習する知識】ぼうグラフ,
「-」
／
Q.棒グラフの目盛りがよめない
わり算で求めてみます
グラフの縦軸で数字が分かる箇所の差を求めます。その差の数を分けてある目盛りの数でわります。その答が１めもりの大きさです。