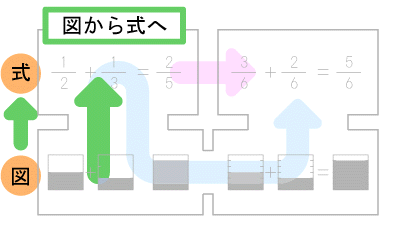
図にこだわって教えるのは、算数における数とイメージを結びつけるためです。今回の記事では、分数のたし算を例に図をつかい教える流れを説明します。
理想的な算数力・数学力
算数の学習ピラミッドがあって、その理想は左の図です。しかし算数が苦手な子の場合、そのピラミッドは凸凹だったりします。
その分かれ目は、数のイメージ理解です。どのようにすれば、美しい学習ピラミッドができるのか。
そこで今回、まず、凸凹ピラミッドになってしまう教え方【失敗例】=数のイメージ理解が育まれない教え方から説明します。
数のイメージが理解ができない教え方
1まず式を見せる
まず、子ども(学習者)に問題を見せます。この問題を見たお子さんは計算の方法を想像するでしょう。そして自分なりに仮説を立てるはずです。
2.お子さんが予想する
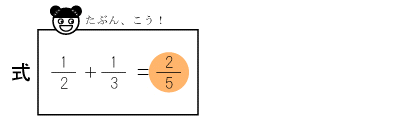
そこで上のように考えます。一桁どうしのたし算の印象が強いお子さんは、このような考え方をすると思います。
1+1=2
2+3=5
笑ってしまう大人の方もいるかもしれませんが、子どもの立場からみると変な流れではありません。
3.方法を教える
そしてここですぐに異分母の計算方法を教えてしまう。
「分母が異なる場合は、通分をするんだよ。」
これでは子どもは腑に落ちず、そういうものか…とイメージ理解がなく身につけようとします。お子さんは「はじめにもった予想ではなぜダメなのか」の納得もえられません。
では、どうすればいいのか?
つぎにしっかりとした算数の学習ピラミッドがつくられる数のイメージを軸にした教え方を説明します。
数のイメージを軸にした教え方
1.図をしめす
はじめに図(イメージ)をみせます。そして次に
「この図を分数の式で表現してみよう。」
と促していきます。イメージから数に書き換えることが、算数数学の第一歩です。
2.図から式へ
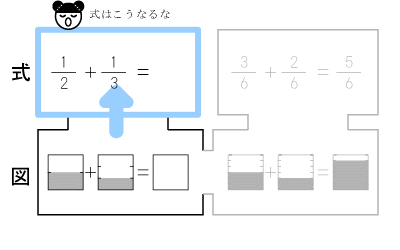
そしてお子さんが図(イメージ)を分数で表現します。ここで初めてイメージと数の関係が分かります。「5分の2になるんじゃないか?」という予測があってもかまいません。
3.図式のアプローチ【式から図へ】
そしてこの式の答を探るために、ここで、もう一度、図にもどってみるように促します。たし算の本質的な意味を、この図で確認します。
「2つをたしたら、結構、いっぱいになる!」
これに気づけば、「5分の2という答は違うなぁ・・・」と検討がつきます。
そしてなぜ、答が分からないのか?本質的な課題に直面します。
「2つの目盛が違うから、どのくらいになるのか分からないのか」
と小さな発見をします。大人からみれば当たり前のこと。しかしこの発見が分数理解の要です。
4.イメージで理由を得る
目盛が違うから分からない・・・ここまでくれば、「目盛がそろえればいい」という発想が出てくるのは、時間の問題です。
まずは、自分で図に目盛をふる。そして本当にその目盛であっているのか、何度も自分で確認します。このような確認動作は本質の理解へとつながるので大切です。
3-5.図式のアプローチ【方法を知らずに導く】
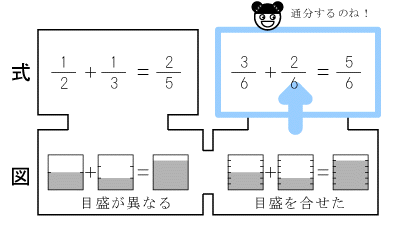
目盛が合ったところで、今度は図を式で表現します。ここで現れた式は、通分された式となります。方法を知らずとも式をたてることができました。
この「方法を知らずにできた」という体験が算数学習において大切です。その経験の後、初めて「通分」の話が生きてきます。(通分のアプローチは省略します)
6.算数指導の理想
“通分”とは「方法」
“目盛を合せる”とは「理解」

これらが2つあって始めて算数力は身につきます。これまでのアプローチは、「概念」「理解」「方法」すべてを踏まえています。
冒頭にあげた「算数力の理想」に照らし合わせるとこうなります。このアプローチは概念→理解→方法という流れをしっかり組んでいます。
概念から、理解。そして方法へと進む。図で考えるとは、傍からみると無駄な寄り道のような気もしますが、自分の頭で考えられる理想的な算数(数学)力を培ううえでとても大切です。
4.図式の由来【※補足】
ぼくが提唱する「図式」とは、このアプローチの重要な箇所、図から式にすすむ過程、を表しています。概念の確認は、子どもに教える上でもっとも重要なことです。