中学受験の算数における食塩水の問題に対して、ビーカー図を使った解き方を紹介します。
【問題】( )に入る数を求めなさい。 武蔵中学入試問題
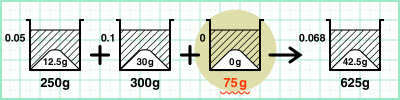
5%の食塩水250gと10%の食塩水300gと水( )gをまぜると、6.8gの食塩水になります。
1-1.問題文に線をひく
まず、問題文を3回、読みます。ここで注意を促すのは「何が、どうなるか?」です。
そして<何が><どうなる?>の部分に線を引きます。
5%の食塩水250gと10%の食塩水300gと水( )gをまぜると、6.8gの食塩水になります。ポイントをまとめます。
では、さっそく図であらわします。
1-2.ビーカー図をかく
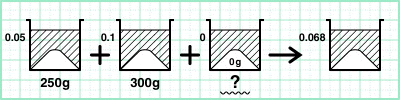
2つの食塩水と1つの水を混ぜます。その3つをあわせるビーカーを用意します。
そしてパーセントは小数で表し、ビーカーの左に書きます。
「5パーセントは0.05。10パーセントは0.1。水には食塩が入っていないから0gだな。」
こんな具合に。問題が尋ねているのは水の量です。そこは「?」にしておきましょう。では、とりあえず、分かるところから考えてみましょう。
2-1.食塩の量をもとめる<1・2番目のビーカー>
さて、解いてみましょう。
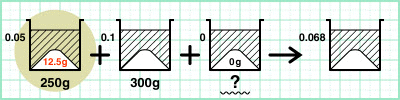
「まず…左のビーカーだ。食塩水の量と濃度が分かっている。
ということは、食塩の量がわかるな!食塩の量は、食塩水×濃度だから」
[式]250×0.05=12.5g
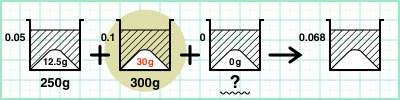
お、10%の食塩水も食塩水の量と濃度が分かっているな。
もういちど、食塩水×濃度を計算しよう。
[式]300×0.1=30g
2-2.全体の食塩の量を求める
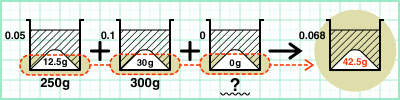
食塩水2つと水をまとめて入れるんだ。ということは、中に入っている食塩も合わされているよな。
4番目のビーカーの食塩の量は、こうなるだろう!
[式]12.5+30+0+=42.5g
2-3.混ぜた食塩水の量をもとめる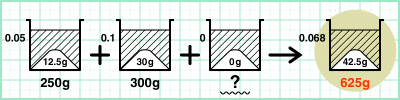
最後の食塩水の食塩の量が分かったぞ。濃度が分かっているわけだから、こんな式が立てられるな。
□g×0.068=42.5g
この四角の部分(□)を逆算で求めてみよう。
[式]42.5g÷0.068=625g
2-4.水の量をもとめる
「全部足した食塩水が、625gなんだよな。
ということは、他の食塩水から引いてしまえば水の量が出るぞ。」
[式]625-250-300=75g
ということは、水の量は75gだ!
まとめ
この解説は、「食塩水×濃度=食塩になる」が理解できている前提の子へのものです。もちろん、この問題の前に図の書き方を学び、食塩の濃度についてしっかり理解します。