図式指導法による公立中学の数学の授業支援。
連立方程式にて驚くべき結果がありました。
塾に行っている子よりも、行っていない子の方が・・・
■学年正解率の度数分布
突然ですが、以下のグラフを見てください。
これは図式指導法をつかって授業支援を行った
公立中学校の正解率度数分布表です。
約100名の生徒さんそれぞれの平均正解率を算出し、
パーセントが高い順に度数(人数)をグラフで表しています。
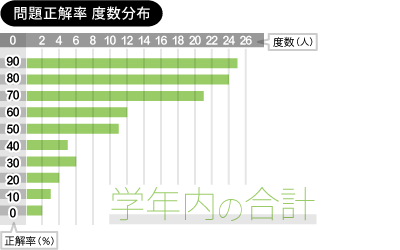
ほぼ正解率が高い順に、度数が高くなっているのが分かります。
このようなグラフの場合、
大多数の生徒が授業の中身が理解できたと予想されます。
■学校外学習の有無を調べてみた
実はこの連立方程式において
正解・不正解を報告する達成度表でこんなアンケートをとりました。
学校外学習の有無(生徒達が塾・家庭教師から習っている)です。
そこに意図があった訳ではありません。
結果を分析していく中で、
なにか発見があるのではないか?
と私なりに考えたからです。
そしてアンケートによると
学校外学習を行っている生徒は、全体の40%。
通常、通塾率というのは70%ぐらいと言われています。
これについて教科担当のI先生も
「こんなに少ないとは思いませんでした。」
と言っています。
学校外学習の有無は、学習量の差を引き起こしいます。
それが成績においても差が出てくることは、察しがつきます。
■学校外学習の有無による
正解率を調べる
しかしです。
正解率の度数分布を、
学校外学習の有無で分けてみました。
すると驚くべき事実が判明したのです。
それが以下のグラフです。
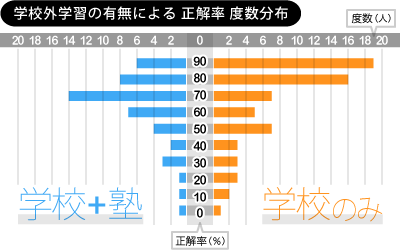
なんと高い正解率をはじき出していたのは、
学校の学習のみの生徒達だったのです。
90・80%以上において、
通塾者の2倍以上を占めています。
■図式指導法の良さ
学校外学習を行っている生徒と、
そうでない生徒は人数そのものが異なります。
ここで簡単に
「高い正解率をはじき出したから、
図式指導法はいい!」
とは私は言いたくありません。
ただ、図で考える数学・算数というのは、
何も知らない状態から学習すると驚くほど自然に理解できます。
「なんでこんな簡単なことが、
教科書や問題集では難しく書くのかな?」
という声が出てくるほどです。
今回、学校外学習を受けていない生徒たちは、
はじめて連立方程式の文章問題に触れました。
前もって解き方を習ってなかったからこそ、
学校外学習の生徒たちよりもすんなり解けた、
受けて取れるのではないでしょうか?
■課題も発見
しかしこのような結果は、
図式指導法の課題もあらたに見えてきたと私は思います。
学校外学習の生徒たちは、
図式指導法に戸惑いを感じたのではないか?
と私は考えるのです。
塾と学校とでは学習が異なる。
それで混乱が生じることでもあります。
また正解率が低い生徒たちへの対策も、
正解率がとても高い生徒たちへの対策も、
課題だと思います。
これほど高い正解率であれば、
教科書レベルの問題が簡単すぎた生徒も多数いたのでのではないか?
とも考えています。
このようにいろんな課題があるのです。
これを次の連立方程式の学習支援機会に、
ぜひ生かして生きたいと思います。
