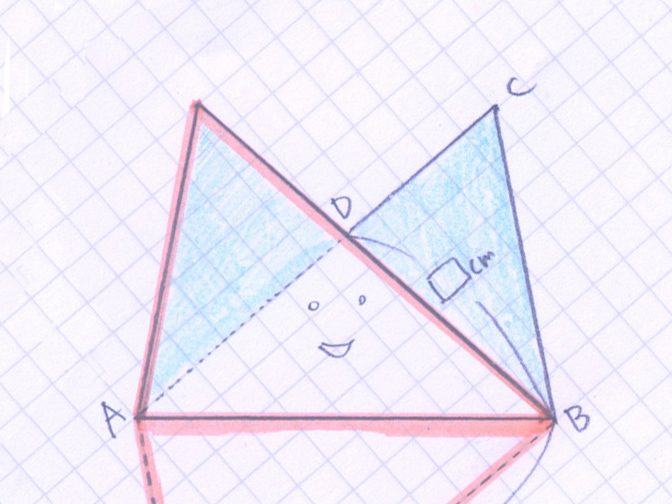
中学受験の算数で図形問題が不得意な子は「平行四辺形の対角線の折曲げ問題」は解くのを避けたがります。自明の理や法則がみつけにくいからです。そこで今回、ぼくのひと工夫した「ねこの耳」をつかって解説してます。
平行四辺形の対角線折曲げ
平行四辺形の対角線の折曲げ問題は、以下のような形をしています。平行四辺形といえば、錯角やら同位角を使った問題が多く、子どもたちもそこに注意を払います。しかしここは折曲げの問題。しかも対角線の折曲げ。
大切なのは、2組の合同の存在です。
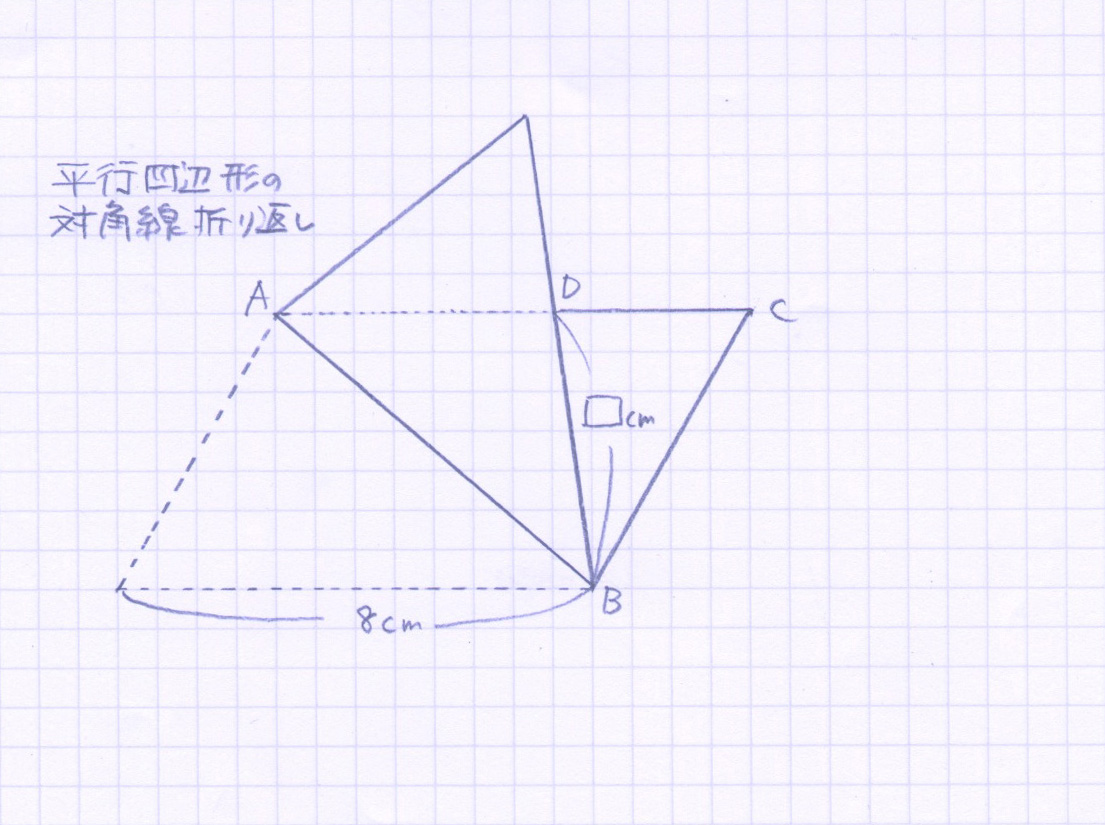
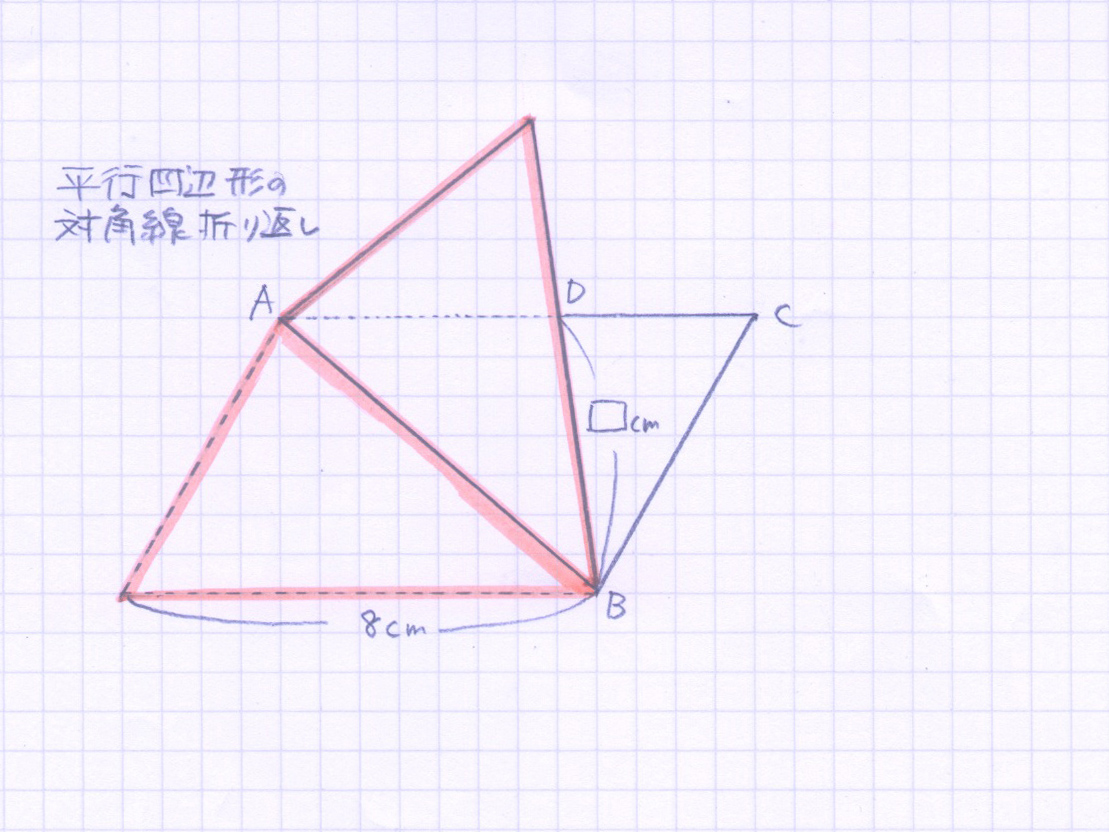
折曲げ部分の合同
一組目は、図形の折曲げ問題であれば必ずある「折曲げた部分の合同(オレンジ色)」です。これは当たり前なので、軽視されがちです。でも必ず等しい辺や、等しい角を記入してもらいます。※今回は見づらくなるので書いてません。あと[ ]cmは今、気にしないで下さい。
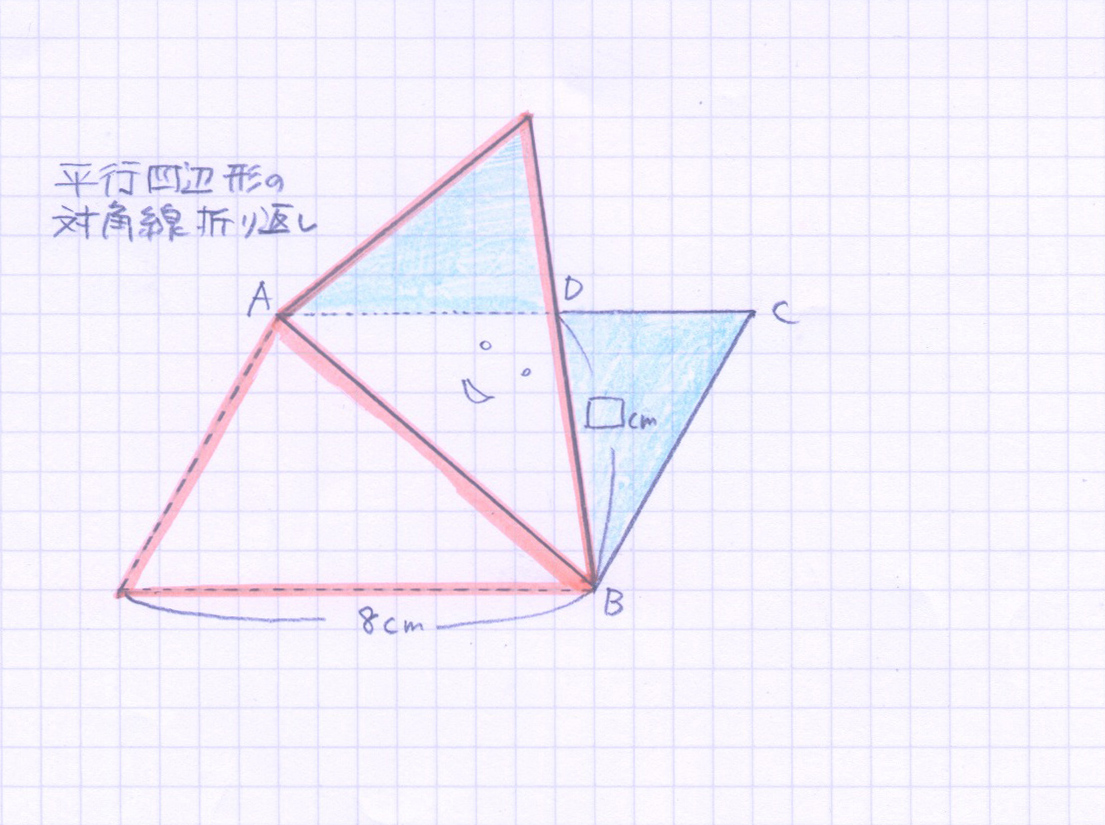
重ならない図形部分の合同
もう一組の合同は、対角線で折曲げた時に「紙が重ならない部分(青ぬり部分)」です。
これは平行四辺形の対角線で折曲げたときに生じる特別な合同ですね。これは見逃されます。分かりにくいです。そこでぼくは、三角形ABD部分に顔をかいて「ねこの耳」として印象づけて説明します。
ねこの耳だなんてずいぶんのオフザケですが、算数が不得意な子、特に図形を探るのが苦手な子についていえば、こんな印象深い比喩が効果的です。算数学習も楽しくなります。
法則の前提から考える
ここから条件を追加してみます。例えば三角形ADBと三角形CBDの面積比が3:2だった場合を考えて、[ ]cmを求めてみましょう。
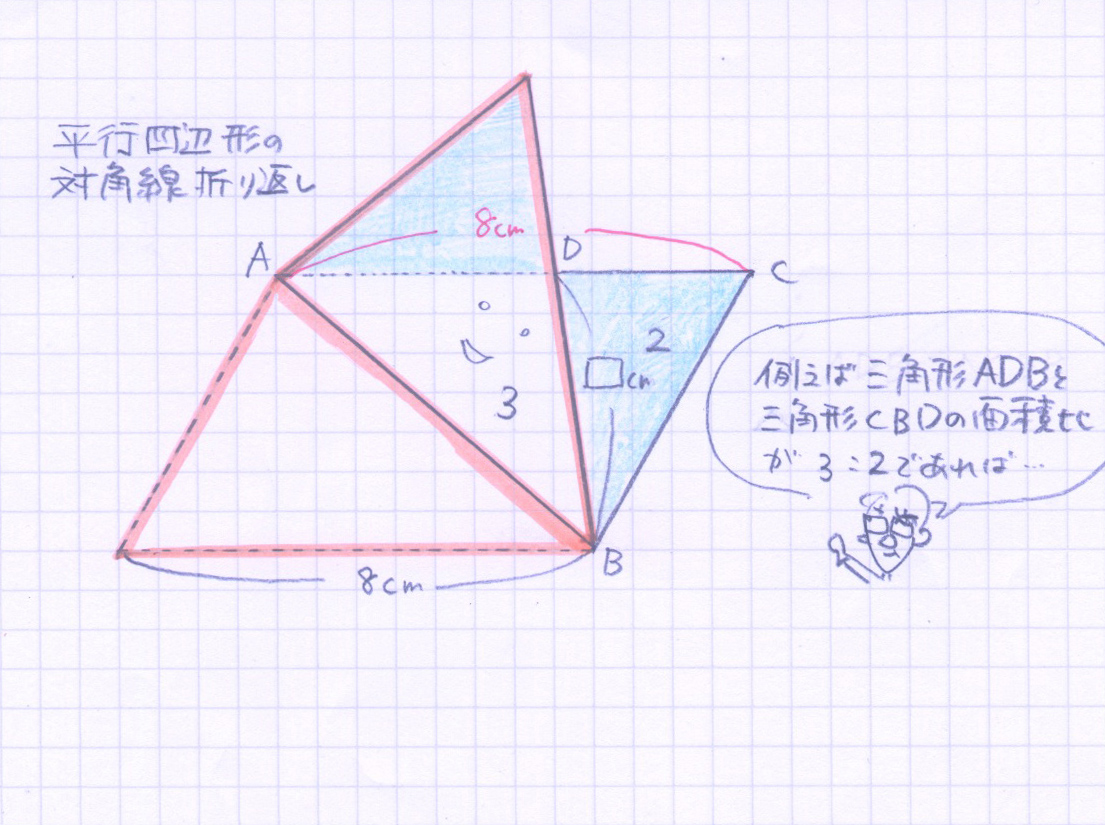
面積比から底辺の比を求める
ここで三角形ADBと三角形CBDは底辺が同じで高さが同じです。「高さが同じ三角形は面積比と底辺の比が等しくなる」という法則を適用します。
実際の指導では、この法則を思い出すことも難しいため「底辺がそろって頭がゴッツンしている三角形って高さが同じ。だから底辺の比が面積比と同じになるんだよね」と解説してますね。
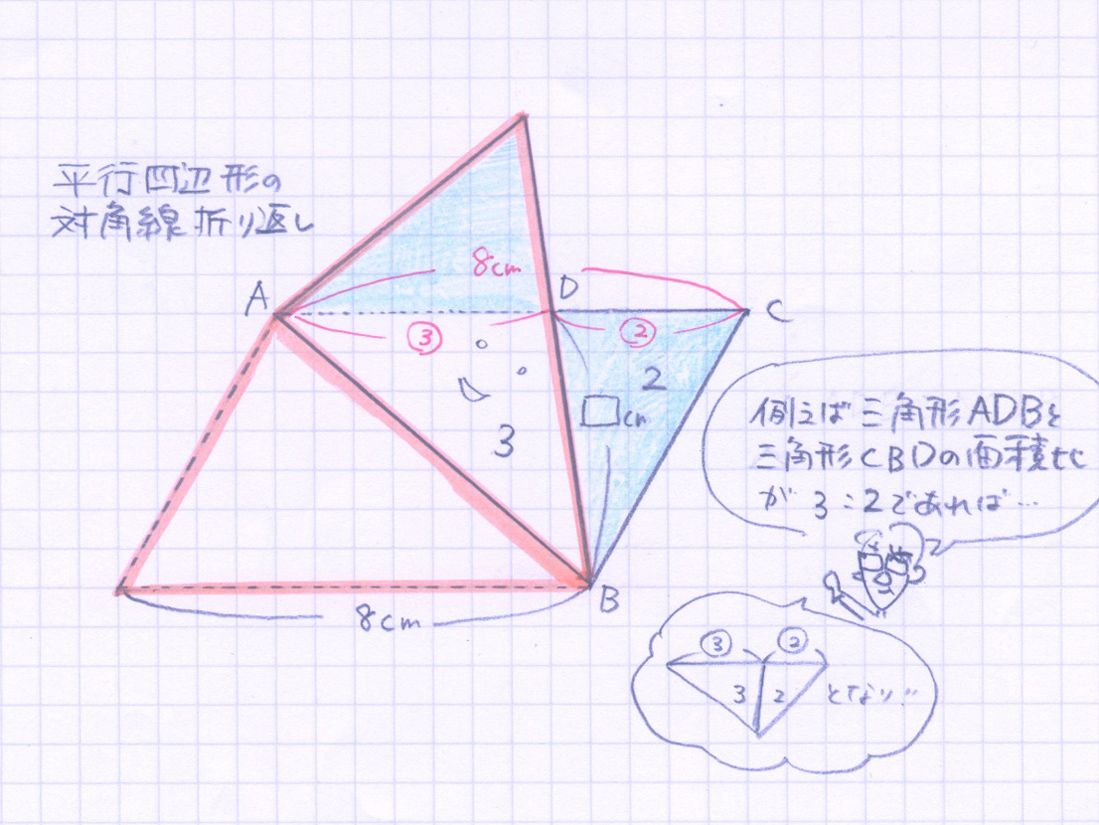
合同だから比も同じになる
ここで青部分の三角形は合同なので、ADとDCの比は対応する辺でも同じとなります。
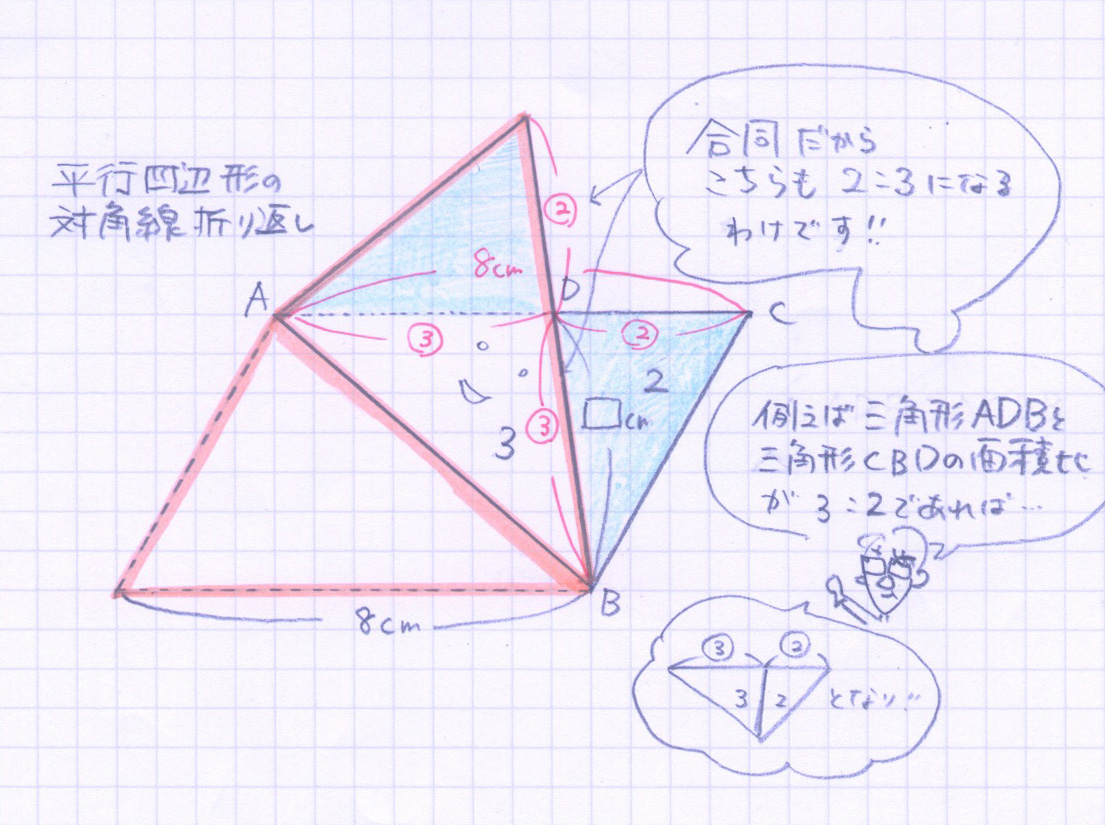
これらの比をつかって、AC8cmを③:②にわけるわけですから、8÷⑤=1.6cm(←これが①に相当)
そして問題となるDBは1.6×③=4.8cmと分かります。
「適切な色分け+キャラだて」で学ぶと分かりやすい
図形が不得意な子を教える際、特に配慮すべきことは「適切な色分け」です。色分けされると合同や等しい部分などが見えやすい。それだけでなく法則が視覚的に自然に身につきます。
あとできれば「キャラだて」があればいいですね。ここでは、合同な存在をねこの耳として青色で表現しています。何度も言いますが、このような具体的なイメージの方が、子どもたちにとって印象深くそして楽しく解けます。特に女の子はこのようなキャラ立てが好きですね。
平行四辺形の対角線の折曲げ問題が出たら、ぜひ「ねこの耳」と唱えながら色で書き込んでみてはいかがでしょうか?きっと楽しいですよ。