苦手な子へのイメージを使った学びについて簡単に説明します。
まずはよくある学習形式を説明した後にぼくが実施している「図で教える方法」を説明します。
■1-1.よくある学習形式【式を見せる】
まず、子ども(学習者)に問題を見せます。
そして子どもなりに仮説を立てるはずです。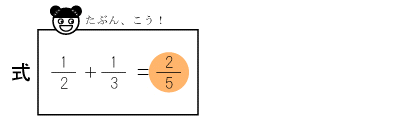
そしてこのあとで計算手続きを教えます。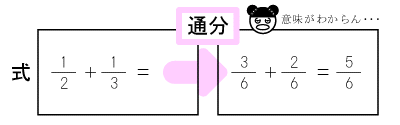
しかしこれでは子どもは納得できません。
なぜなら、明らかな自分なりの仮説があったからです。
そこでみかん先生の教え方(図式)をご紹介します。
■2-1.図式のアプローチ【図から出発】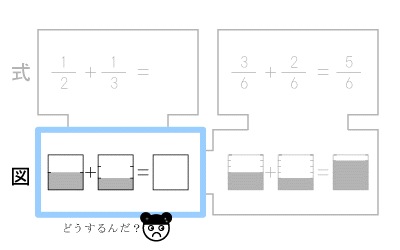
図式では、はじめに図(イメージ)を与えます。
イメージが理解の導入にふさわしいからです。
そして次に「この図を分数の式で表現してみよう。」
と子どもに出題します。イメージから数へうつる算数数学の第一歩です。
■2-2.図式のアプローチ【図から式へ】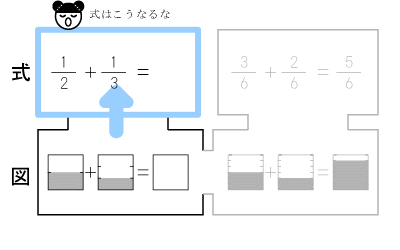
そして子どもが図(イメージ)を分数で表現します。
ここで初めて未知の分数のたし算を、目で確かめます。
もちろん、「5分の2になるんじゃないか?」という予測もありです。
子ども達の自由な発想を、ここで押さえつけるようなことはしません。
■2-3.図式のアプローチ【式から図へ】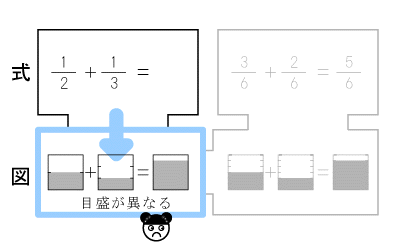
そしてこの式の答を探るために、ここで、もう一度、図にもどってみるように促します。
なぜならたし算の本質的な意味を、この図で確認できるからです。
「2つをたしたら、結構、いっぱいになる!」
これに気づけば、
「5分の2という答は違うなぁ・・・」
と検討がつきます。
そしてなぜ、答が分からないのか?
本質的な課題に直面します。
「2つの目盛が違うから、どのくらいになるのか分からないのか」と小さな発見をします。
大人からみれば当たり前のこと。
しかしこの気づきこそが、分数の要なのです。
■2-4.図式のアプローチ【本質理解を得る】
目盛が違うから分からない・・・
ここまでくれば、「目盛がそろえればい い」
という発想が出てくるのは時間の問題です。
まずは、自分で図に目盛をふる。
そして本当にその目盛であっているのか、何度も自分で確認します。
このようなたった数秒の確認行為が「本質理解」を手に入れるのです。
■2-5.図式のアプローチ【方法を知らずに導く】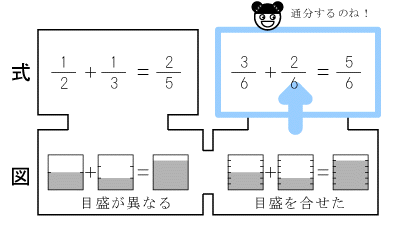
目盛が合ったところで、今度は図を式で表現します。
ここで現れる式は、通分された式です。
答も図を使って、方法を知らぬままにできました。
この「方法を知らずにできた」という経験が大切です。
その経験の後、初めて「通分」の話が生きてきます。
(通分のアプローチは省略します)
■2-6.僕のアプローチ【算数力の理想】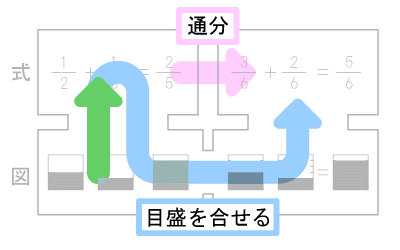
“通分”とは「方法」
“目盛を合せる”とは「理解」
これらが2つあって始めて算数力は身につきます。
そしてお気づきの方もいるかもしれません。これまでのアプローチは、「概念」「理解」「方法」すべてを踏まえています。こういったことが「算数力の理想」になるのです。
このアプローチは概念→理解→方法という流れをしっかり組んでいるのです。
だから子どもも無理なく方法を吸収できます。
■3.図式の由来【※補足】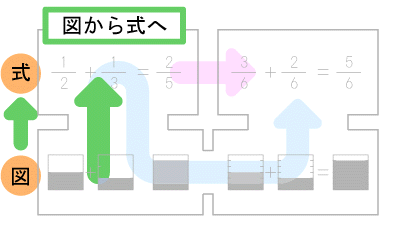
私が唱えている「図式」とは、このアプローチの重要な箇所、図から式にすすむ過程、を表しています。概念の確認は、子どもに教える上でもっとも重要なことです。
