3+2=32にしてしまう…長さを定規で計れない…など子どもの思いもよらない躓きにどう対応すればいいのか?それぞれの原因(要因)はさまざま。そんな中の主な原因に対する対応方法を簡単に書いてみました。
「色の異なる散らばったおはじきで、どっちが多いか尋ねてもかわからない。」
低学年では、異なる2つの量を対応させて判断すること(1対1対応)ができないお子さんもいます。このお子さんは、そのとき見た印象を優先します。以下の手順で示すといいでしょう。
- 色の異なるおはじきを1つ1つ対応するように整列させます。

おはじきを丁寧に並べます。
- おはじきが対応して並んでいることを指で確認します。

おはじきを丁寧にゆびで確認します。 - 対応している対象物を整列させて、視覚的に個数の違いを示す。

赤色のおはじきが黄色のおはじきより多いことを指で示します。
「女の子3人、男の子5人、子どもは何人?の問題ができない。」
上位概念(“子ども”という上位概念は、女の子・男の子という下位概念を含んでいます)が引き出せていない可能性が考えられます。解説シート「上位概念と下位概念」(A4紙/PDF/無料)を使って解説手順を説明します。
- 子ども(男女いる)大人がいる絵をみせます。

- 大人をゆび指して「この人は子どもですか?」と尋ねます。お子さん:違うと首を振る
- 「男の子はどこにいますか?」と尋ねます。おはじきを置かせます。(指でさしでもOK)

- 「女の子はどこにいますか?」と尋ねます。おはじきを置かせます。

- 「男の子は子どもですか?」「女の子は子どもですか?」と尋ねます。どちらも「はい」という答が得られたら、次へ進みます。
- 「子どもはどこにいますか?」と尋ねます。お子さんにおはじきを置いてもらいます。

- 最後にまとめます。

男の子と女の子、大人と子どもを視覚的に示します。具体的に身近な人も登場させて話してあげるといいでしょう。
この上位概念は徐々に身についてくるものでもあります。慌てずに丁寧に扱って下さい。
「3+4=34としてしまう。」
たし算の考え方が「数字をくっつける」と誤っています。「数字が意味する数量イメージをくっつける」に正してあげます。式の数字の上に ●●●+●●●●と補助のイメージを加えたプリント「イメージつきたしざん」(A4紙/PDF/有料)を使って説明します。
- 「数字は●の数を表しているの」と指で示します。
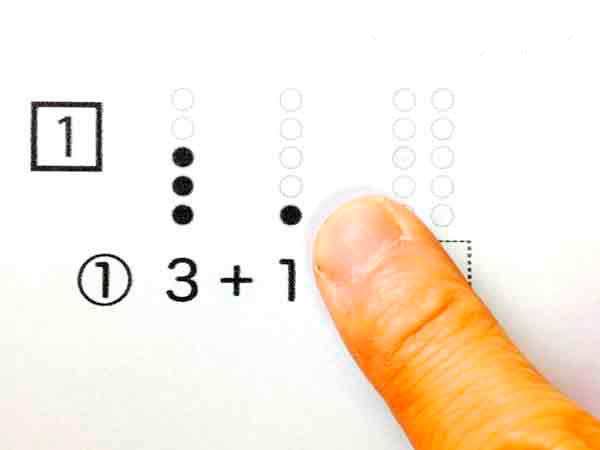
数の上に黒丸を加えてもいいでしょう。 - 「数をたす(+)というのは、この数字の●を合わせることだよ。合わせた●を答の上にかいてみよう」と促します。
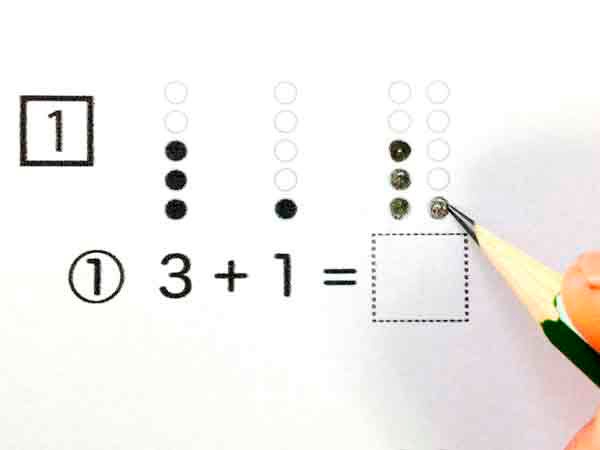
丁寧に黒丸をぬります
「じゃあ、ここに合わせた●の数を、数字で書いてみよう」と促します。
黒丸を見て数字を書き込みます。
「9の次は10になることが分からない。」
まだ数記の概念を理解していないようです。以下の手順で教えます。
- 1から10まで指で数をカウント
指やおはじきで「いち…に…さん…じゅう」と唱えながら、数えます。このとき数字表示は教えません。 - 位のへやを見せて9を示す。
ブロックが9こあり、数の表示が9であることを確認します。
1ブロックの部屋にブロックが9個ある - 「じゅう」になることを示す
つぎにブロックを1こ増やして「じゅう」になることを確認します。
1ブロックの部屋にブロック9個に1個加えた状態 - 「ブロックは10こ集ったら、へやを移ります」となりの部屋に移ることを知らせます。(この時、じゅうの棒はフラフラなので寝かせるよ…とぼくは言ってます)そして数の書き方を教えます。

1ブロックの部屋を出て、じゅうの部屋に移った状態
このとき「じゅう」が2ほんなら二十、3ほんなら三十と大きな数について触れてもいいです。
「定規で1cmや1mmを正しく掴めない。」
 従来の定規は1cmと1mmが混在しています。特にcmについてはメモリが打たれていますが、ミリは自分で把握しなければなりません。これが混乱の元です。
従来の定規は1cmと1mmが混在しています。特にcmについてはメモリが打たれていますが、ミリは自分で把握しなければなりません。これが混乱の元です。
まずは、ミリとセンチが単位として分かれている定規「ミリとセンチが分かる定規の型紙」(A4紙/PDF/無料配布)をご利用下さい。
「3cm4mmの長さを書くことが出来ない。」

3cmと4mmを順を踏まえて教えます。
- 3cmのメモリを打点しそこまで書きます。
- そこからさらに4mm鉛筆を移動させます。
ミリとセンチが色分けされている定規「ミリとセンチがひきやすい定規の型紙」(A4紙/PDF/無料配布)をご利用下さい。
「定規を使って、直線がうまくひけない。」
問題は「定規そのもの」と「持ち方」が考えられます。
- 定規は、できるだけ太くて短いものがいいです。
- 持ち方は、抑えるべき箇所にシールを張るといいでしょう。
「定規を使って、長さが計れない。」
段取りが把握できていない可能性があります。絵柄がないシンプルな定規に変えて、0の所に赤マジックで印をつけます。
- 線に定規を合わせる
- 線の端に赤印を重ねる
- 計測する
段取りメモを横目にゆっくり練習して下さい。
「10の補数を覚えられない。」
補数は5組(1と9・2と8・3と7・4と6・5と5)あります。以下の手順で段階的に扱っていきます。
-
- 「十の補数イメージ表」で、それぞれの数をイメージでとらえます。このとき6〜9の数については5の数(◯部分)に◯がいくつ加わっているかよく掴めるようにします。
- 「十の補数イメージ表」で補数の組合せを覚えます。右列を隠して、左列を答えます。逆もします。
10の補数イメージ表 ◯ ◯◯◯◯◯◯◯◯◯ ◯◯ ◯◯◯◯◯◯◯◯ ◯◯◯ ◯◯◯◯◯◯◯ ◯◯◯◯ ◯◯◯◯◯◯ ◯◯◯◯◯ ◯◯◯◯◯ - 「十の補数表」を使い、左列を隠して、右列を答えます。逆もします。
- 「十の補数イメージ表」で、それぞれの数をイメージでとらえます。このとき6〜9の数については5の数(◯部分)に◯がいくつ加わっているかよく掴めるようにします。
| 1 | 9 |
| 2 | 8 |
| 3 | 7 |
| 4 | 6 |
| 5 | 5  |
- 学習プリント「10をつくる(10の補数)」(A4紙・PDF)で補数チェックをします。
子どもにひき算をうまく教えられない。
ひき算は「大きい数−小さい数」の大原則は大切。そしてひき算を教える上で大切なことは「その答が何を指しているか?」を示すことです。これは言葉ではなくイメージがいいです。今回、イメージでひき算を導入する学習プリント「ひきざん」(A4紙/PDF/無料)を使って説明します。
- ひかれる数(式の前)の数を数でいいます。
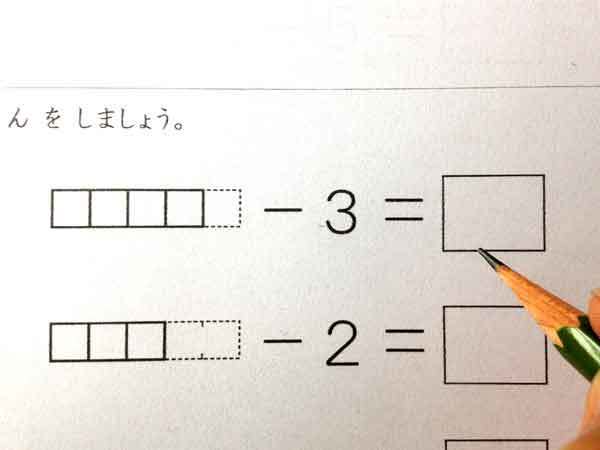
- ひく数の分だけブロックを鉛筆で消します。
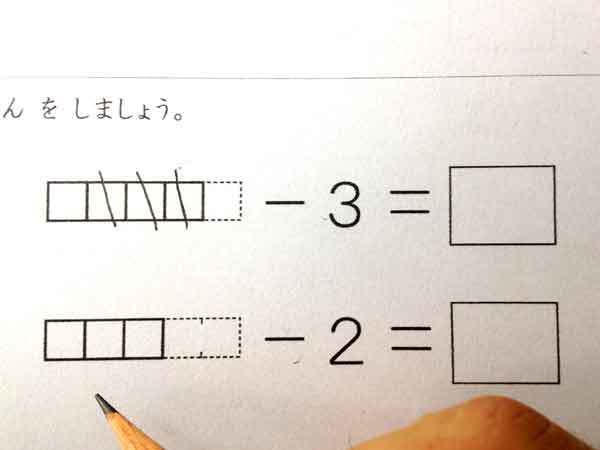
ひく数をみてブロックを消します ※このときブロックを鉛筆で消すのではなく指で隠しても構いません。

ひく数だけブロックを隠しても構いません。 - 残ったブロック(見えているブロック)の数を数えて、答えを書きます。
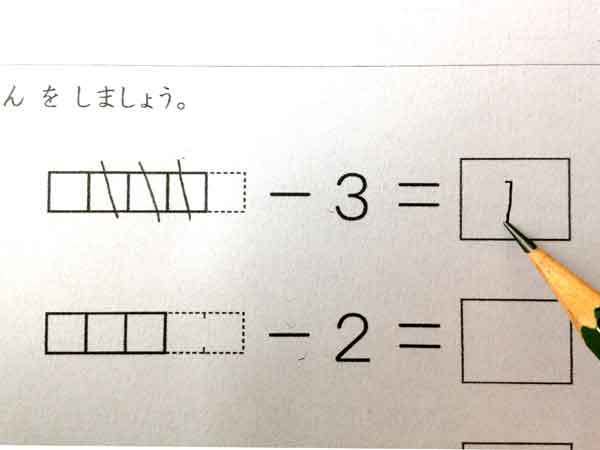
消された(隠された)数を答に書き込みます。
以上です。この後にブロックを数に変えて、普通の数字のひき算へと移していきます。
10が3こで13と答える。
言葉から数へのイメージが不十分です。10(じゅう)と3(さん)をみて反射的に13(じゅうさん)と処理を行っています。
- 10と3
- 10が3こ
10と3は指しているものが異なりますので、10はブロックで表現して文章の意味を正確に捉えさせるといいでしょう。学習プリント「10をいくつ」(A4紙/PDF/有料)で学習してみて下さい。
字がマスからはみ出てしまう。
子どもの手先の器用さを考慮していくつか工夫が要ります。
- 大きめのマスに変える
- 計算などを1行あける
はみ出たからと叱ってはいけません。
「簡単なグラフ(2年生)に整理することができない。」
まずは、以下の工夫を試みてみるといいと思います。
- グラフの縦線を太くして横線と区別をつけてみる。
- 表のラベルをイラストを含めてかいてみる。
これでもできない場合は、1年生の内容のグラフにさかのぼって学習する必要があります。
「1円玉が5枚で、5円玉になることが分からない。」
お金の枚数と価値の数量を区別して考えることができていない。また、数の世界を順序数としてのみ捉えている可能性もあります。1円をブロック1枚,5円はブロック5枚と枚数に変わる具象物で価値のイメージを培う必要があります。ブロックにお金の色を塗るとさらにお金と価値量を直観的に判断できるようになるでしょう。
「繰り上りのたし算ができない。」
“たした答に「じゅう」がついたら、そのじゅう(1)は次の位に書く”と指導するといいでしょう。説明するだけでなく1つ1つ手順をふんで教えます。
「繰り下がりのひき算ができない。」
“引けなかったら、隣の位(部屋)から(手をさし出して)10をもらう”と教えるとイメージしやすいと思います。イメージがつかない子もいますので、数と位のしくみ(23は10ブロックが2つで、1ブロックが3つ)を示してあげると納得できると思います。
「時刻(アナログ盤)が読めない。」
算数セットにあるアナログ時計は、ふつう短針と長針が別の色となっています。短針(時間)と長針(分)は別に教えるといいでしょう。(※改めて詳しく解説したいと思います。)
「時刻の『〜分前』『〜分後』が答えられない。」
過去の記事(時刻の前後が分からない子どものいいぶん)で詳しく説明しています。そちらをごらん下さい。
「午前と午後を理解できない。」
朝起きた午前中に「短針が12をさすまでが午前ね」と話した上で、正午を過ぎ「これまで午前だったけれど、ここから午後」と教えます。午後から午前になる0時については理解するのは後々でいいと思います。
「2けたのたし算で7+21=91と書いてしまう。」
位どりが意識されていません。1ブロック7つと、10ブロック2つ&1ブロック1つを用意して、合わせるといくつになるか確認します。すると1ブロック同士を合わせて計算することに気づくと思います。慣れるまでは1の位の数を色をつけさせて計算をさせるといいと思います。
「九九が完全に覚えられない。」
忘れがちな九九を単語帳に書いて繰り返し唱える。とてもシンプルな方法ですが成功の確率は高いようです。また、忘れた時の対応方法を身につけることも大切です。
- 数を入れ替えて考える(例:3×5なら5×3で考える)
- その下の数を考えてたす(例:4×8が分からないなら、4×7を考える)
このような対応力を身につけることも大切です。
「302と198を比べると198が大きいと言う。」
それぞれの数字が大きいものを、数が大きいと見ています。まずは、数の規模をイメージするために302と198をブロックで示し、どちらが多いかを判断させましょう。
「上の位が大きい数字の方が、数は大きくなる」ことを十分に確認します。
「dLやLの単位、cmやmなどの単位がごちゃごちゃ。」
単位がただの“着けたし文字”になっている可能性があります。日常生活の見えるところに、その単位が示されているものを用意して、Lはかさ、mは長さを表すものと把握できると思います。
「205-58の繰り下がりで一の位が百の位から数を受け取ってしまう。」
いわゆる“2段繰り下がり”と言うものです。一の位が十の位に「10ください」と手を差し出す。しかし十の位は空っぽ。だから十の位は百の位に「10ください」と手を差し出す。百の位は2が1になり、十の位は一の位に10を差し出すから、10が9になる。“位の手は長くないから一の位から百の位には手が届かない”と話すと納得してくれる場合があります。
「直角がない四角形を三角形に間違えることがある。」
図形の角に色で◯印をつけます。角の数を数えてもらいます。「4つ角があるときは四角形。3つ角があるときは三角形。」と説明します。眺めるだけでは印象優先が働きますので、手順化して判断条件に落とし込むことが大切です。
「たし算の文章問題ができない。」
たし算が用いられる文章題にはいくつかのパターンがあります。後日、詳しく解説します。
「ひき算の文章問題ができない。」
ひき算が用いられる文章題にはいくつかのパターンがあります。後日、詳しく解説します。
「直角三角形が分からない。」
正三角形は形として1つに定まる特別な三角形ですが、直角三角形も1つに定まるものと捉えているかもしれません。「3つの角の中に直角な角があれば、直角三角形になる。」と教えて、1つ1つ判断させるといいと思います。
「五千二百七を527と書いてしまう。」
漢数字をそのまま数字に置きかえて処理しているようです。まず位の境に線(五千/二百/七)をいれます。
位には千・百・十・一があることを確認し、その上で上の位から1つ1つ書いていきます。「〜十がないから十の位は空っぽ。だから0を書く。」と教えるといいと思います。
「立体の面の数を正確に数えることができない。」
立体を手に持ち面を数えると、分からなくなります。まずは、立体を平面上において、上→横→底と順を追って面に印をつけて数えるといいでしょう。
「自分で展開図を作図して立体を作ることができない。」
子どもがいきなり展開図を作ることは難しいでしょう。まずは、立体になるお手本の展開図を切りとり、立体を作ってみる。次にお手本の展開図(切り取られた立体)を元にして、少し変えて展開図を作図して切り取る。この繰り返しで立体と展開図のイメージが重なりあいます。空間把握力は時間が必要なので、じっくり取り組む姿勢が大切です。
その他の学年の算数の意外な躓きへの教え方
