頭をこねくり返して諦めて。しばらくして「あ!」と気づく。算数はこれがあるから面白いです。
ズームの授業を終えたと同時に、娘がぼくに算数の宿題をもってきました。
「ねぇお父さん、これどう思う?」
学校の宿題プリントでした。彼女が指さした問題文は「12㎠の図形をかきなさい」でした。
「どうかけばいいんだろう」と娘。
「それで悩んでいるの?」
「うん」
宿題プリントの他のところを見ると、面積を求めることはできていました。面積が広さを意味していることも分かっている様子。
それならば、たぶんできます。この問題文の解釈を「12マス分の図をかいてください」と換えればいいだけ。
でもそれでは面白くありません。
本人も嫌いな算数です。ぼくはここでじっくり考える経験をして欲しい。
そこで「折角だからさ、斜めの線で12㎠の形を作ってみようよ」と娘へ提案しました。娘も了解。
それからしばらく頭を寄せ合って面積を考えました。
「これは2㎠だね。これは4㎠だね」
直角三角形を作りました。
「この直角三角形の面積はわかる?」
しばらくして3㎠だとわかりました。
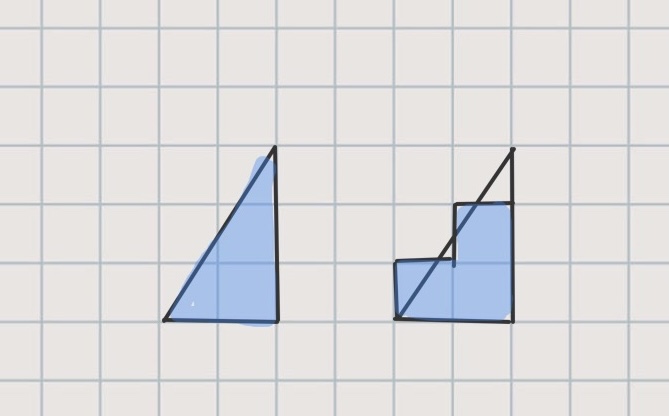
そしてアイデアが生まれました。12㎠であれば3㎠の三角形を4つ組み合わせればできます。
斜辺の長さは全て同じなので正方形になるはずです。サラサラと書いてみました。
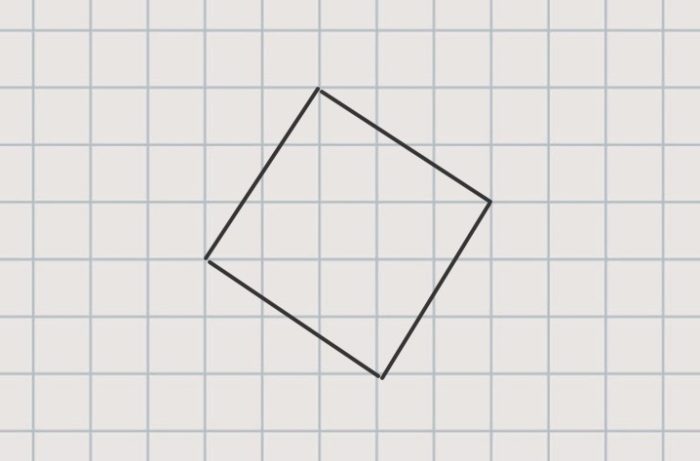
しかし書いてすぐに「あ、ごめん。この正方形は12㎠ではない」とぼくは呟きました。
「え?なんでできないの?」
「よーくみて。ここ」
正方形の真ん中に1㎠のマスがあるのです。三角形の隙間に隠れている。
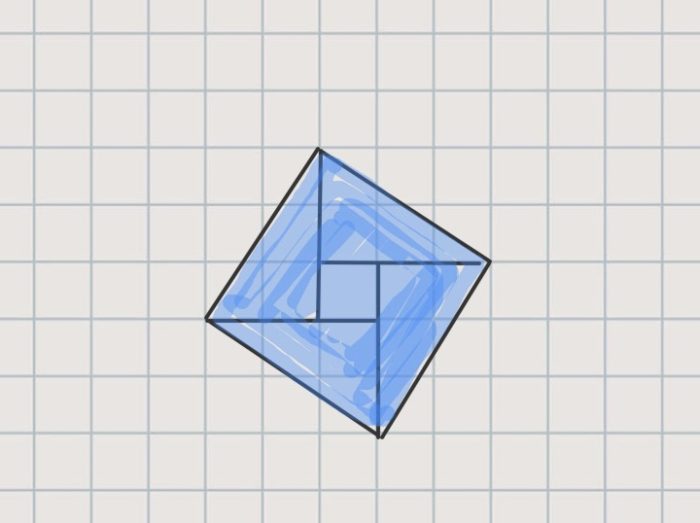
「ほんとだ!」
「これ13㎠だね。うーん残念…」
折角ここまで考えたのに。というわけで斜めの正方形は諦めて、普通の12マスの図形をかきました。
それから夕食のとき。
娘は名残惜しいのか「あーこれも12㎠かぁ」とまたプリントの図形を眺めていました。
その図形には、穴が空いていました。
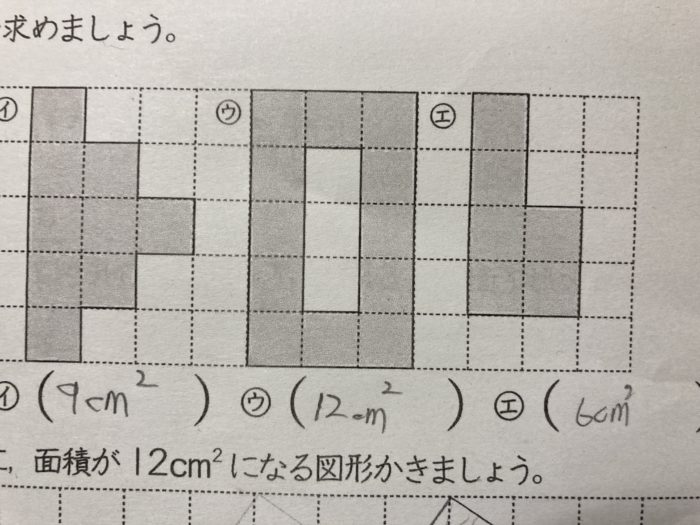
「あ!」
偶然。ぼくと娘は同時に叫びました。考えていることは同じでしょう。
娘はさっきのプリントを出して、ぼくと一緒に考えた13㎠の正方形をかきました。
そして中の1㎠の方眼をくりぬきました。これで12㎠です。
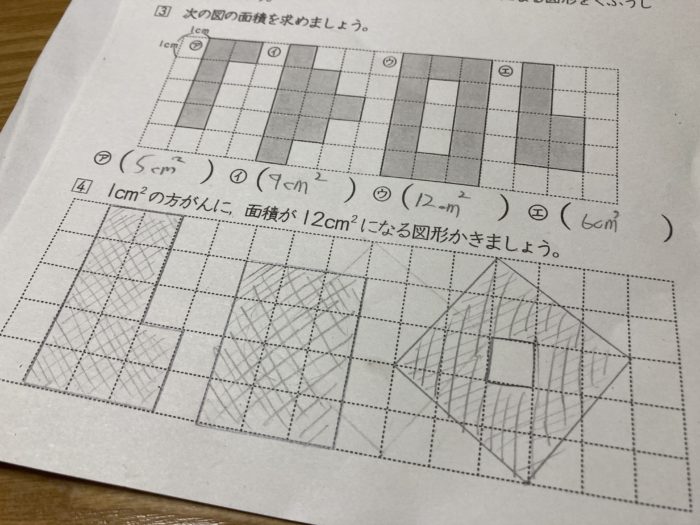
娘はとても満足そうでした。そしてなんで気づかなかったんだろうと、二人で大笑いしました。
算数は、こういうところが面白いです。
娘は今年、5年生です。
高学年にもなると、まわりの子たちの多くは受験塾へ行ってどんどん先を習います。当然、嫌な思いをすることもあるでしょう。
でもわが子には、こういうアレコレと考える時間を大事にしてあげたいです。

