東京在住のHさん(中学1年)のズームの授業です。
単元は一次方程式です。
すでに学校で学んだそうです。そこでぼくがまず確認したのは「計算式」と「方程式」の違いです。
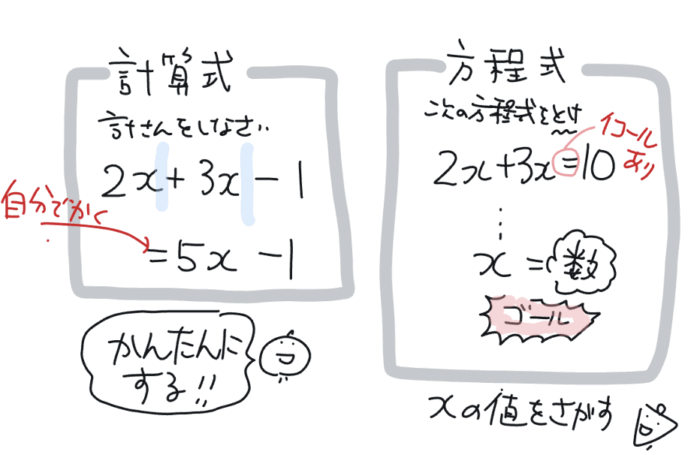
「計算式」は、複雑な式を計算して、簡単な文字式・数にする。
「方程式」は、未知数(例えばX)の値を求める。
その違いを「問いの文」「ゴール」を見比べてみます。
大体、こんな反応が返ってきます。
え、似たようなものだと思ってた!


うん、似ているからね
そう、このような勘違いがあるんです。だから「計算式・方程式の違い」はたびたび授業で説明します。

ちなみに学校ではしないと思います
そしてここからです。
ワーキングメモリが低い子は、この方程式によって大きく混乱しだします。計算式のやり方と方程式のやり方がごっちゃになるのです。
そのごっちゃ状態で、教科書の例題を解くとますますごっちゃになります。
ですから、まず方程式の基本的な動作をまとめる。
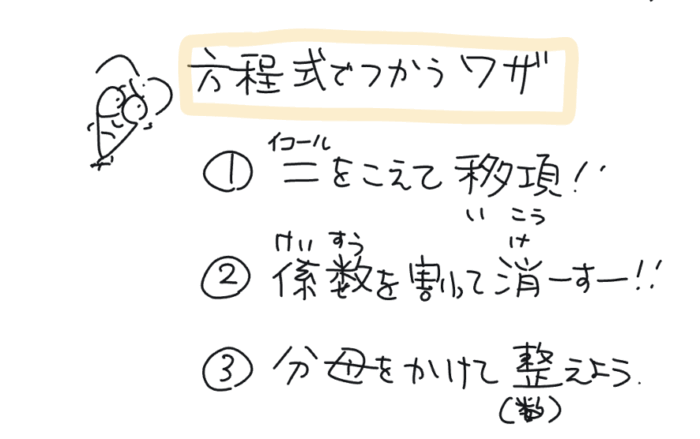
それを意識してもらう必要があります。
そしてひとつひとつの判断ポイントを押さえながら、スモールステップで進んでいくのが理想的です。
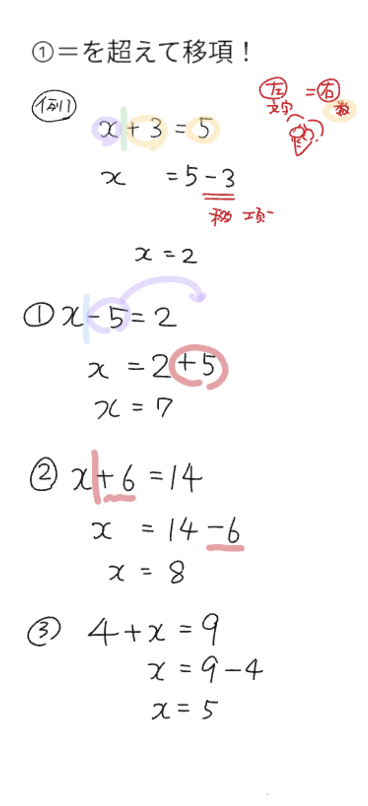

しかし状況は単純じゃありません。
係数処理の場面でこのように教えました。文字の項につく係数で両辺を分数で割るやり方です。

そして練習をしてもらいました。
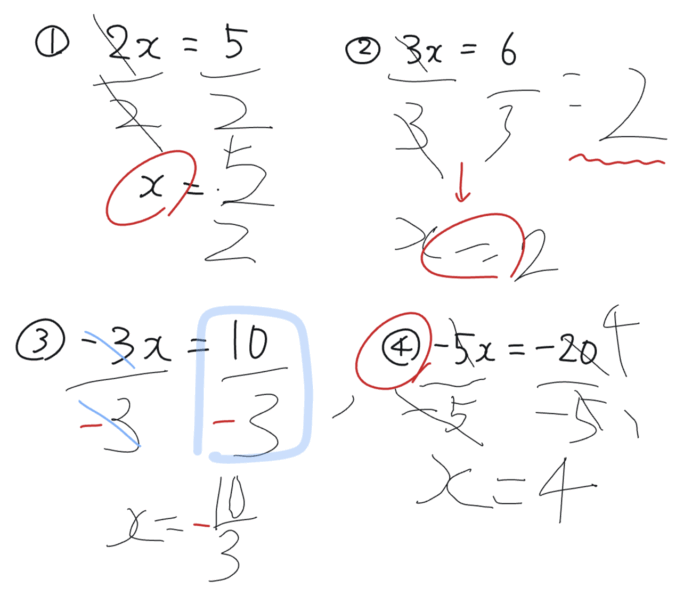
大体、出来ていますね。
ワーキングメモリが弱い(また基数性の概念が弱い)子は、分数を用いた処理が無難です。
しかし時間がすこし空いたら、このように解いてました。
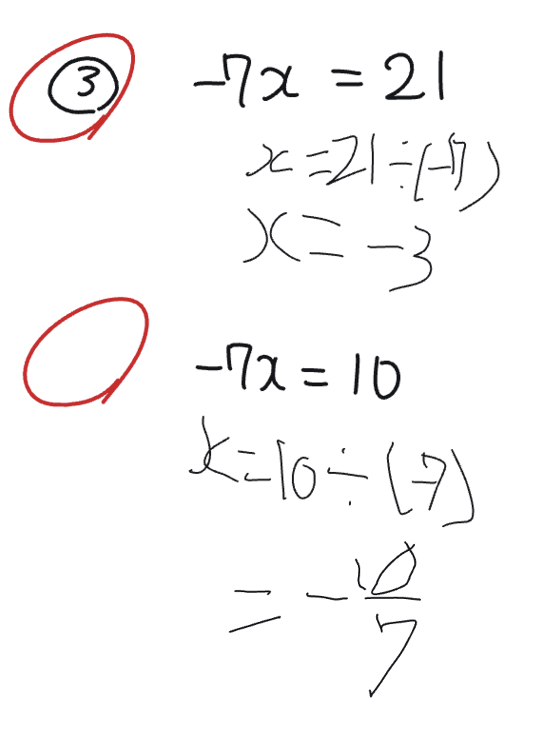

うっ…まずい…変わっている…
なぜ、この解き方に変わったのか。理由は簡単です。その前に学校でそう学んだからです。
もちろん、この解き方も正解です。

このやり方でできているのなら…このままでいいか…。
しかしこの方法だと懸念されることが…
とりあえず、様子をみてみました。そして授業の最後のまとめでこのように解いてしまいました。
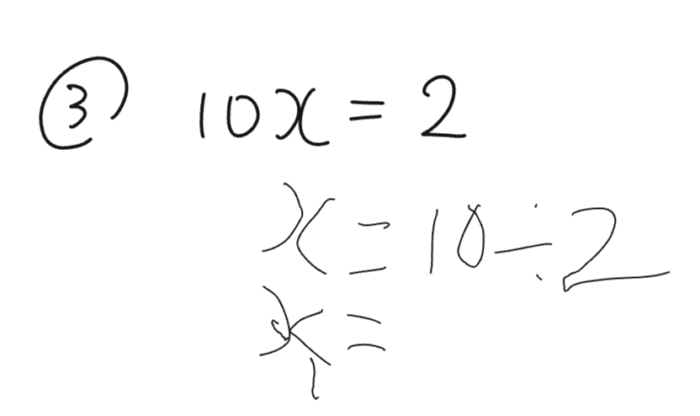

やっぱり!
えっ違うんですか?

10と2をパッとみて割れる方でわり算をしてしまう。
また、10で割るつもりが−10になる。つまり係数の処理ではなく、移項になることもあります。
実はわり算方式だとこのミスを誘ってしまうのです。
このミスは注意し続ければできるようになればいいのですが、なかなか難しい。
本人も頭で分かっても、つい反射的に反応してしまうのです。
ですから、たとえ時間はかかってもミスを誘わない方法をとるほうが無難です。総合的な学習時間も減りますし、定着がいいです。
Hさんの一次方程式の学習ははじまったばかり。
これからまだまだ続きます。粘り強く練習している様子をお母様から伺っています。
これからも頑張ってほしいです。

