このページでは、みかん先生による「数学Aの教え方」をQ&Aで解説しています。
1.場合の数
Q.円順列はふつうの順列ではダメなのか分かりません

円順列は「唱えて同じものは排除」です。
「回転すると一致する並び方は同じ並び方である」という説明に納得がいかないのでしょう。「位置が違うんだから、並びだって違う」と思ったのではないでしょうか。
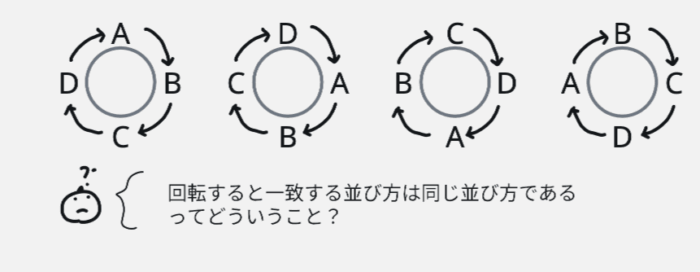
円順列は「円」です。円には、はじまりと終わりがありません。スタートをA から唱えると「A→B→C→D→A→B→C→D→A→B…」と続きます。Bをスタートで唱えると「B→C→D→A→B→C→D→A→B…」と続きます。
これ、どちらも同じ音ではありませんか?
理由は、見た目の位置が違っても並びが同じだからです。円順列は回転しつづけたときのならびの数です。それで位置は違っていても、円の中では並びが同じだからふつうの順列ではないのです。
Q.9人を部屋A.B.Cに3人ずつ入れる時と、3人ずつの3組に分ける時の計算が異なるのか納得できません。

組の場合、同じメンバーはダメなんです
部屋ABCに分けるとき、部屋Aに「①②③」となることもありますし、部屋Bに「①②③」となることもあります。これらはメンバーが同じでも部屋が異なるので別としてみます。
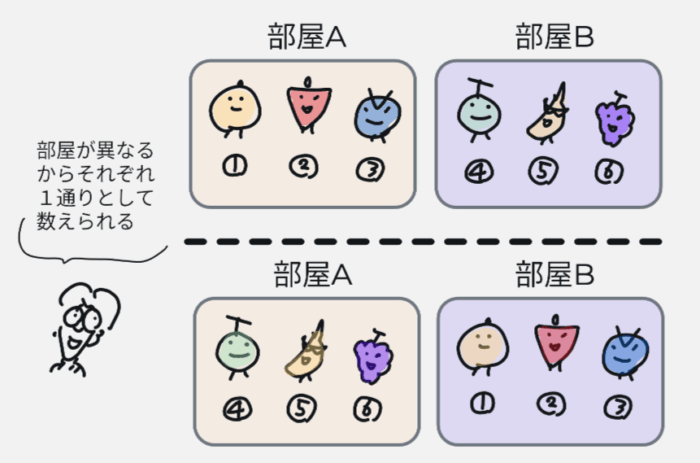
しかし3人ずつ3組で分けるときは「メンバー」に注目してます。3組のメンバーが同じものは認められません。
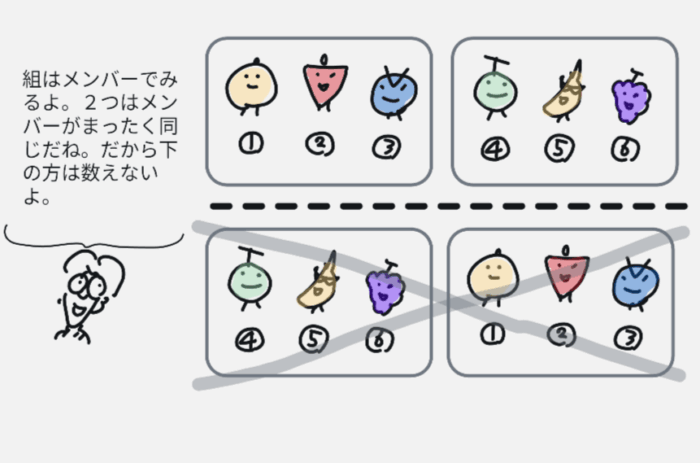
それで部屋分けと組み分けは計算が異なるのです。
(部屋わけの通り数÷組数の階乗をすることで、同じメンバーのパターンを消しています)
Q.区画を進む道順の総数がなぜ「同じものを含む順列」なのか分かりません

行動順が複数の「進む・曲がる」が決まるからです
どの道順でも右に3回、上に2回進むことは変わりません。
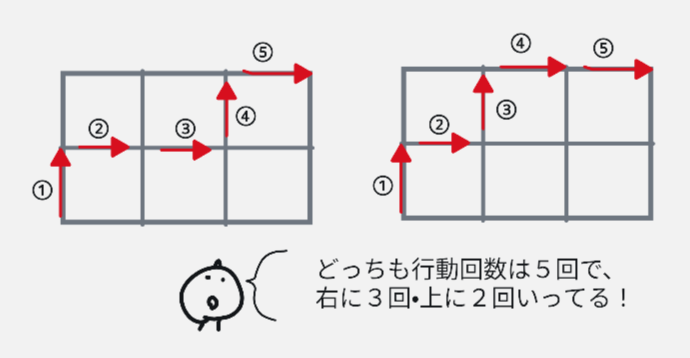
ここで考え方を変えます。
行動番号①から⑤までに、2つの動作(上2・右3)をくばる話として捉えます。するとこれが同じものを含む順列であることがわかるはずです。
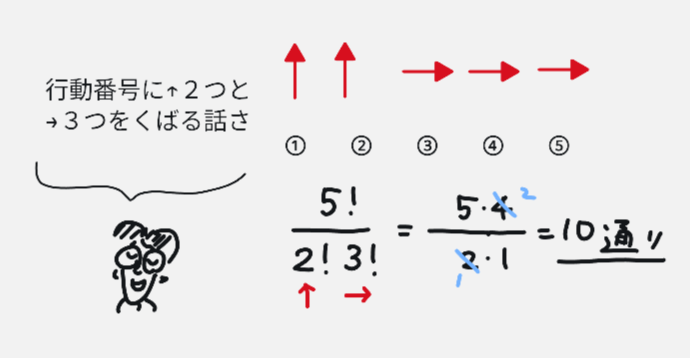
実際にその順列を書き出してみることをお勧めします。そうすることでより深く理解できます。
Q.反復試行の公式が覚えられません

具体的な例を通してイメージで覚えましょう
目の数が6こあるサイコロを5回転がして、2が3回出る確率を考えます。
1回の試行で2が出る確率は1/6ですね。これが5回中、3回出るのを簡単にイメージしましょう。
その上で意味を考えます。
「2が3回出て、2が出ない確率」は1通りだけじゃない。全部で5C3通りある。
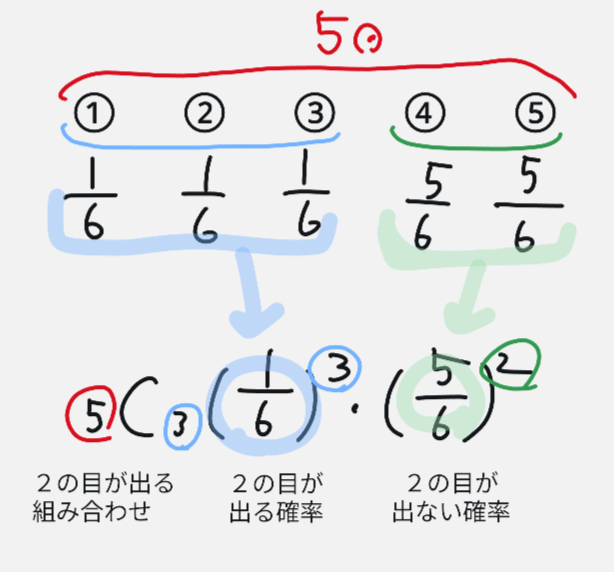
複雑な公式は暗記するよりも、具体的な例を通してその意味を理解した方が記憶に残りやすいです。
2.図形の性質
Q.メネラウスの定理が覚えられません

キツネの顔を飛び跳ねるノミの話で覚えましょう
メネラウスの定理はまず名前から難しそう。実際の公式の中身も分数の上下にアルファベットが、だだだっと並んでいます。文字列で暗記は大変です。
そこで紹介したいのは「キツネの顔をノミが飛び跳ねる話」です。飛び跳ねる線分の長さが、分数の①〜⑥に入ります。
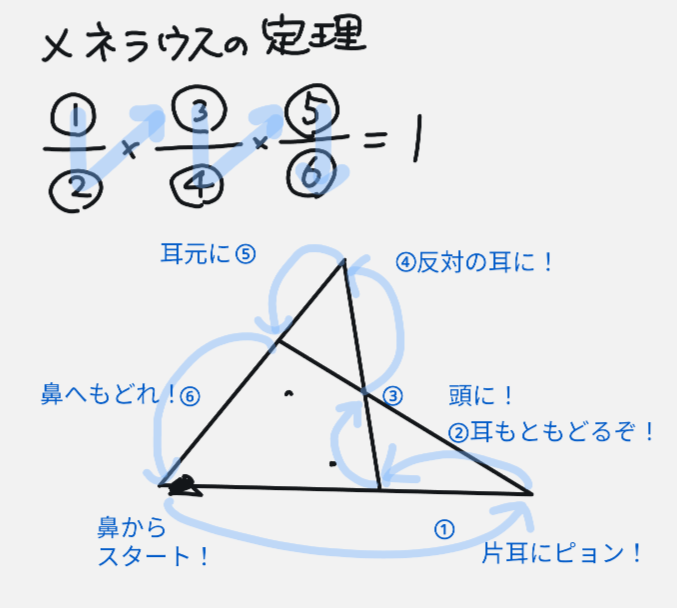
これは動作で覚えますので、右回りだけではなく、左回りも可能です。
Q.方べきの定理(3つ)が見抜けませんし、定理も使えません

交点・円周点のかけ算が等しいと覚えましょう
方べきの定理そのものは簡単ですが、形が異なると一気に難しくなります。
まず「円と交わる2直線が生み出す定理」であることを理解。これが一番大切です。
その上で、2直線(下の画像だと赤線・青線)の交点から、円周への線分を考えます。
その線分を掛け合わせたものが等しい。それだけです。
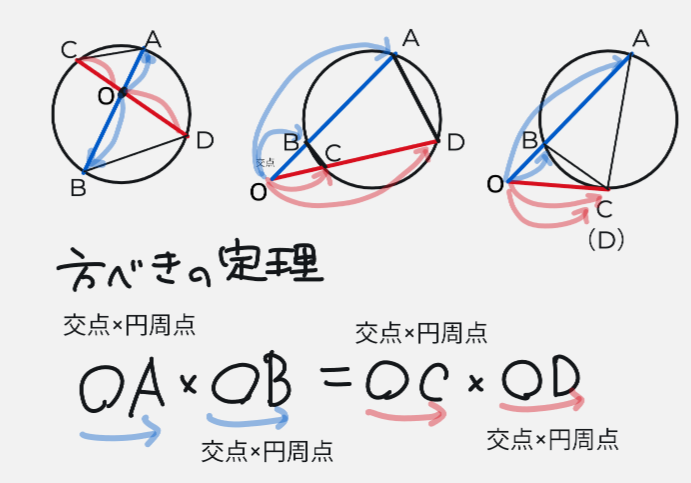
交点・円周点のかけ算が等しいと覚えましょう。
Q.2つの円の位置関係(5個)が混乱します

5つの関係を数直線でまとめて覚えましょう。
一般的な参考書では表でまとめています。しかしその5パターンを覚えるのが難しいです。
そこでおすすめしたいのは、円の位置関係を数直線と絡めてまとめて覚える方法です。それが下になります。
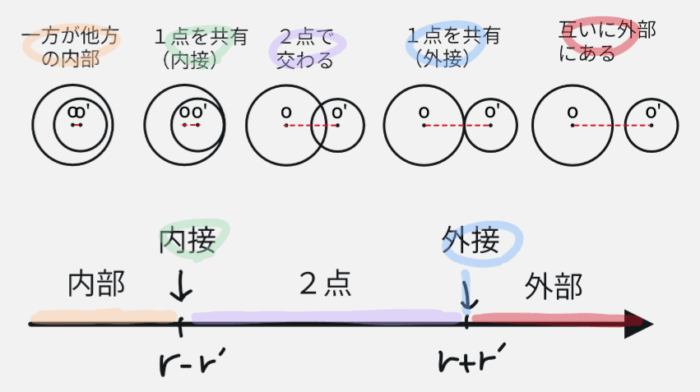
「大きな円の半径(r)+小さな円の半径(r’)」と「大きな円の半径(r)ー小さな円の半径(r’)」を求めたら、それを上の数直線に反映します。
あとは半径間の距離が数直線のどこにあたるのか見れば一目瞭然です。
3.整数の性質
Q.素因数分解で約数を求めるやり方がわかりません

因数を縦に並べて組み合わせです!
約数はその数を割り切れる数です。その割り切れる数は、その数の「因数」。その因数を組み合わせで作ればいいです。
たとえば56の素因数分解をします。それぞれの因数を下に書き並べます。あとはその組み合わせを考えましょう。
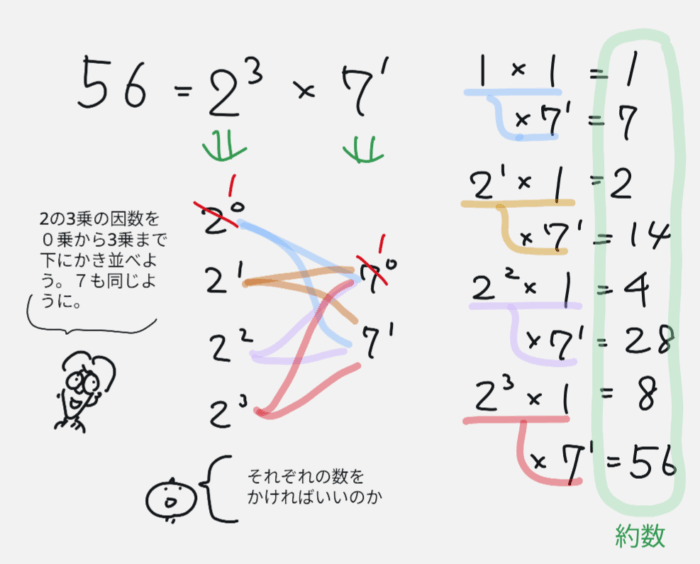
これを理解できれば、約数の個数は4×2=8個というのもすぐわかるでしょう。
Q.ユークリッド互除法で、どのようにして最大公約数を求めるのかわかりません。

小学校で習った筆算を使いましょう!
小学校でならった筆算をつかいます。
たとえば408と119の約数を求める場合です。
筆算をつかい408を119でわってあまりがでます。続けて、119を筆算の線をかいて余りの51でわります。
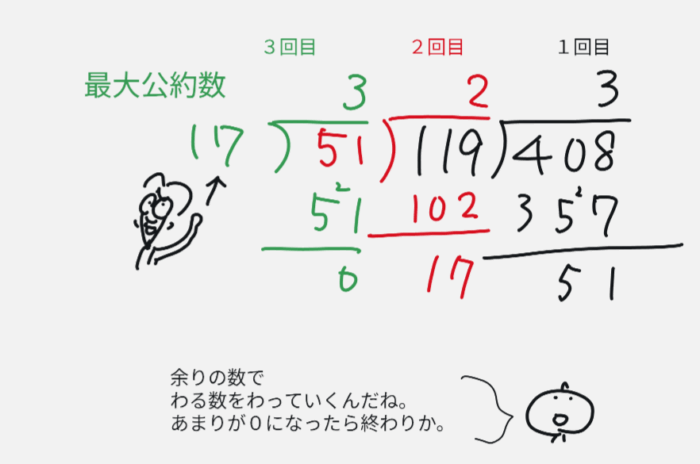
これをあまりが0になるまで続けます。あまりが0になった時のわった数が最大公約数です。
