このページでは、みかん先生による「数学 Ⅰの教え方」をQ&Aで解説しています。
◯目次
1.数と式
Q.因数分解のたすきがけまではできますが、そのあと「何をすればいいのか」わからなくなります。

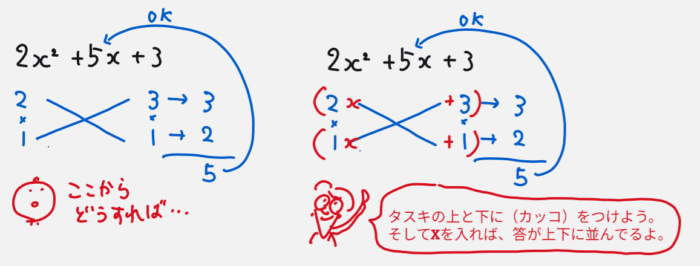
たすきの数をそれぞれくくりましょう
因数分解のたすきがけまでできたなら、上の列としたの列をそれぞれカッコでくくりましょう。そのカッコを横に並べればおしまいです。
Q.因数分解がピンときません

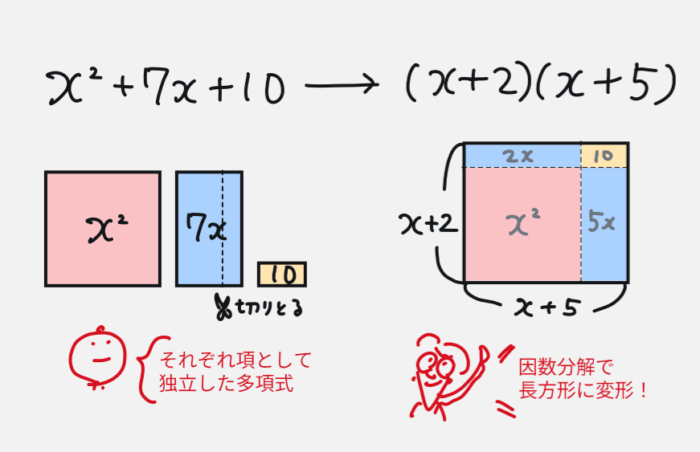
多項式と因数式の違いを理解しましょう!
まず、たくさんの項があるのが多項式。それを全体的にかけ算まとめるのが「因数式」です。
因数式にすることで、二次方程式などがさっくり解けます。
Q.3次式の展開と因数分解の公式(6個)が混乱します

公式の特徴を2つ理解しましょう
この3次式の公式6個の
だと思います。
- (a+b)3=a3+3a2b+3ab2+b3
- (a-b)3=a3-3a2b+3ab2-b3
- (a+b)(a2-ab+b2)=a3+b3
- (a-b)(a2+ab-b2)=a3-b3
- a3+b3=(a+b)(a2-ab+b2)
- a3-b3=(a-b)(a2+ab-b2)
これはすべて覚える必要はありません。3.4と5.6なんて、ただひっくり返っているだけですから。
「(カッコ)3」と「文字3」の公式の特徴を覚えましょう。

2.集合と命題
Q.命題P⇒Qとその対偶の真偽が一致することがわかりません

「日本と東京」で考えてみましょう
例えばです。命題「東京にいれば、日本にいる。」は真ですよね。東京は日本の中にあるからです。
この対偶は「日本にいなければ、東京にいない。」となります。これはどうでしょうか?真です。日本の外にいて、東京にいることはできません。
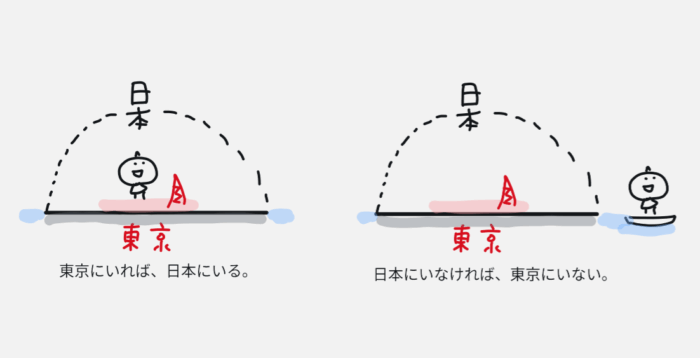
これが「命題の真」と「対偶の真」の一致です。包含関係にある身近な例を考えてください。
3.二次関数
Q.平方完成が途中から混乱します

平方パターンを1つに絞りましょう
教科書をみると平方完成で「係数がないパターン」「分数パターン」「係数があるパターン」など多様で、それぞれ微妙にやり方が違って混乱します。
特に係数があるパターンで中カッコをつかうあたりは、多くの中高生が「どうすれば…」と静止します。

そこで1パターン

この平方完成のやり方だと、全てのパターンで利用できます。
Q.グラフをうまく書けないので、最大値・最小値をもとめられません

表を使って求めましょう
最大値・最小値・値域を求めるだけなら,グラフを書かなくても求められます。
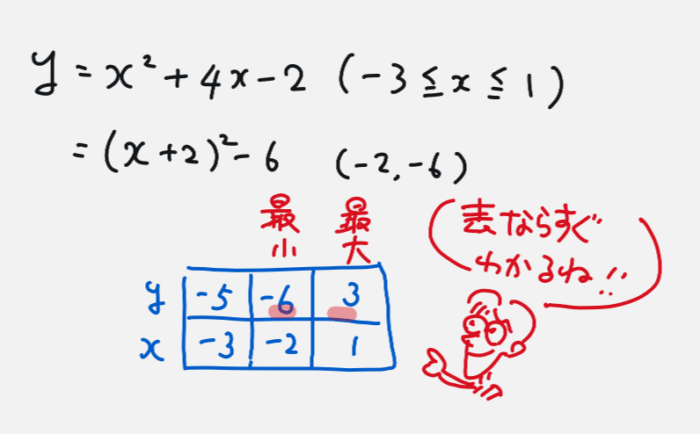
グラフを書くのが苦手な子(時間がかかる子)はおすすめです。
Q.判別式の使いどころがわかりません

実数解の「個数」だけ知りたいときです
判別式にこだわらなくても解の公式をつかえば、実数解の個数はわかります。
でも個数が決まるのは、この解の公式のルートの中が「プラス・0・マイナス」のどれかによってです。
それなら、解の公式の初めの部分(2a分のマイナスb…)をすっ飛ばして、ルートの中の計算だけしてもいいですよね。

実数解の個数の
4.三角比
Q.拡張した三角比の定義がピンときません

直角三角形の辺の長さをプラス・マイナスで捉えましょう
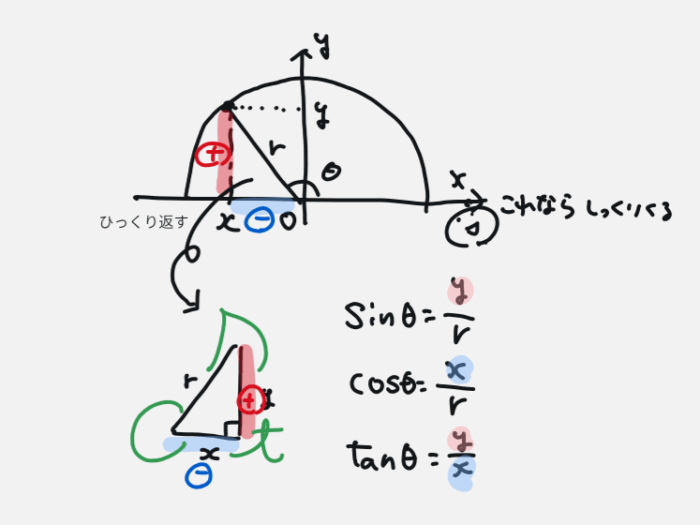
5.データの分析
Q.箱ひげ図の意味がわかりません

集団をざっくり4グループに分けた、だけです
40人の集団を4つに等しくわけると、10・10・10・10となります。箱ひげ図の考え方はこれです。
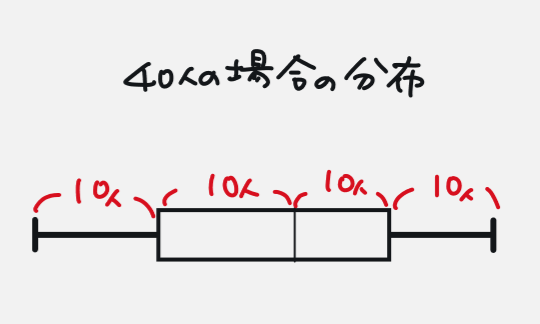
ただし、第1四分位数・中央値・第3四分位数が奇数によって決まった場合、その数だけは4つのグループに入りません。だから「ざっくり4グループ」となると覚えてください。
Q.分散の計算が途中からわからなくなります

式の書き方をひと工夫すれば大丈夫ですよ
まず、平均をもとめる式をズラーっと書いて平均を求めます。

その下に、それぞれの数から平均を引いた数を書いて、同じように平均を求めます。それで出た値が分散です。
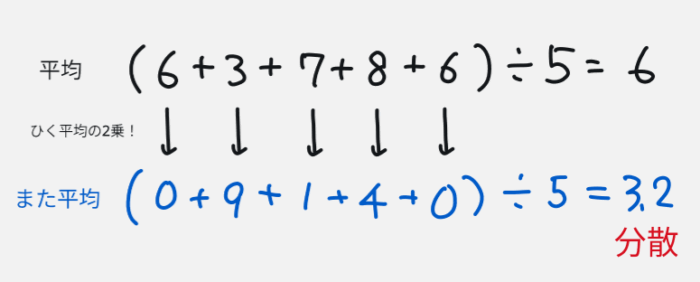
「偏差の2乗の平均」と覚えてしまうのもいいと思います。
